三个主要树种单木生物量及其器官分配模型

引用本文

王冬至, 张冬燕, 蒋凤玲, 许中旗, 张志东, 黄选瑞. 三个主要树种单木生物量及其器官分配模型[J].自然资源学报, 2018,33(8): 1390-1402
WANG Dong-zhi, ZHANG Dong-yan, JIANG Feng-ling, XU Zhong-qi, ZHANG Zhi-dong, HUANG Xuan-rui. Models for Estimating Biomass and Its Distribution in Organs of Three Main Tree Species[J]. Journal of Natural Resources, 2018,33(8): 1390-1402 复制到剪切板

DOI:10.31497/zrzyxb.20170684

Permissions

《自然资源学报》编辑部所有

三个主要树种单木生物量及其器官分配模型

王冬至^1a,², 张冬燕^1a,^1b, 蒋凤玲^1a, 许中旗^1a, 张志东^1a,², 黄选瑞^1a,^2,^*

1. 河北农业大学a. 林学院,b. 商学院,河北保定 071000

2. 河北省林木种植资源创新与保护实验室,河北保定 071000

^* 通信作者简介：黄选瑞（1962- ）,男,博士,教授,研究方向为森林资源可持续经营与管理。E-mail: hxr1962@163.com

第一作者简介：王冬至（1984- ）,男,河北景县人,博士,讲师,研究方向为森林资源可持续经营与管理。E-mail: wangdz@126.com

收稿日期:2017-07-10 网络出版日期:2018-08-20

基金:国家重点研发计划（2017YFD0600403）;林业公益性行业科研专项（20150430304）;河北省教育厅资助科研项目（QN2018125）;国家科技支撑项目（2015BAD09B01）;国家重点研发计划（2016YFD060020303）

摘要

目前已有不同方法构建生物量相容性模型,但基于非线性似乎不相关回归估计法实现不同树种生物量模型相容性及各器官生物量分配模型的研究较少。因此,论文以塞罕坝华北落叶松、油松、白桦3种林分为对象,基于非线性似乎不相关回归估计法和广义多项Logit模型,建立了包含哑变量的非线性可加生物量模型及各器官生物量分配模型。结果表明：不同树种树干生物量模型确定系数均大于0.90,树枝、树叶、树根生物量模型确定系数在0.77~0.93范围内,各器官生物量均方根误差和绝对误差分别在2.68~17.19 kg/株和0.83~1.39 kg/株范围内,经过检验不同树种各器官生物量模型均能满足精度需求。不同树种广义多项Logit分配模型,通过似然比检验、比分检验和Wald检验均达到显著水平（ P<0.001）,各器官参数均表现为显著水平（ P<0.05）。不同树种树干、树枝、树叶及树根生物量比例分别在0.76~0.87、0.07~0.11、0.02~0.07、0.04~0.07范围内。包含哑变量的非线性似乎不相关生物量模型及广义多项Logit各器官分配模型,实现了生物量模型在不同树种间的通用性,并对森林生物量器官分配格局研究提供了科学参考。

关键词: 林分类型; 生物量; 哑变量; 似乎不相关回归; 多项Logit模型

中图分类号:S718.5 文献标志码:A 文章编号:1000-3037(2018)08-1390-13

Models for Estimating Biomass and Its Distribution in Organs of Three Main Tree Species

WANG Dong-zhi^1a,², ZHANG Dong-yan^1a,^1b, JIANG Feng-ling^1a, XU Zhong-qi^1a, ZHANG Zhi-dong^1a,², HUANG Xuan-rui^1a,²

1. a. College of Forestry, b. College of Business. Agricultural University of Hebei, Baoding 071000, China

2. Forest Resources Innovation and Protection Laboratory of Hebei, Baoding 071000, China

Fund:National Key Research and Development Plan, No. 2017YFD0600403;Forestry Public Welfare Industry Research Project, No. 20150430304;Hebei Education Department Funding Research Project, No. QN2018125;Science and Technology Support Project of China, No. 2015BAD09B01;National Key Research and Development Plan, No. 2016YFD060020303

Abstract

At present, there are different methods to construct compatible models of biomass. However, there are few reports on the compatibility of models for different tree species and the allocation model of component-specific biomass based on the nonlinear seemingly unrelated regression method. In this paper, the research objects were Larix principis-rupprechtii, Pinus tabuliformis and Betula platyphylla forests in Saihanba National Forest Farm, Hebei Province, China. Based on the nonlinear seemingly unrelated method and the generalized multinomial Logit model, the nonlinear additive models of biomass with dummy variables and allocation models of biomass in organs were established. The results showed that the discriminant coefficients ( R²) of stem biomass models for different tree species were all higher than 0.90, and the root mean square errors ( RMSE) and absolute errors were in the range of 16.68-17.19 and 0.84-1.07; in the biomass models of branch, leaf and root, the discriminant coefficients ( R²) were in the range of 0.77-0.93, and the root mean square errors ( RMSE) and absolute errors were in the range of 2.58-12.18 and 0.83-1.39. After inspection, the biomass models of different tree species can meet the precision requirement. The generalized multinomial Logit allocation models of different species all reached a significant level ( P< 0.001) after Likelihood ratio test, Score test and Wald test. The parameters of each organ were significant ( P < 0.05). The proportions of biomass in trunks, branches, leaves and roots of different tree species were in the range of 0.76-0.87, 0.07-0.11, 0.02-0.07 and 0.04-0.07, respectively. The models of nonlinear seemingly unrelated regression with dummy variables and the generalized multinomial Logit model of biomass allocation in organs can be used universally among different tree species and provide scientific basis for the study of forest biomass allocation pattern.

Keyword: forest type; biomass; dummy variable; seemingly unrelated regression; multinomial Logit model

文章图片

森林生物量在研究森林生态系统结构与功能^[1]、生产力和生产潜力评价^[2]、物质循环和能量流动^{[3, 4]}、碳循环和气候变化影响与适应^[5]中具有重要意义。然而不同器官生物量及分配规律通常会受到自然因素（光合作用、呼吸作用、枯损与生长等）和人为因素（采伐、修枝等）的影响^[4], 因此, 世界各国越来越重视对森林生物量的估计、监测和评价^[6], 其中生物量建模是项重要基础工作。在树木生长过程中, 各器官生物量生长均呈现异速生长规律^[7], 并在生态学和应用环境学研究中广泛应用^{[8, 9, 10]}。不同器官生物量与分配是表征立木生长过程的重要指标^[11], 对了解树木变异、预测林火、木材生产及养分循环等^[12]具有重要作用, 因此对立木不同器官生物量估计及其分配的研究是必须的。

目前国内外学者已对生物量建模工作做了部分研究, 汪珍川等^[13]、付甜等^[14]基于幂函数模型构建了亚热带主要森林类型地上各器官生物量模型; 然而由各器官生物量之和估计总生物量时预测误差较大^{[14, 15]}。常用度量误差法、转换因子连续函数法和加权生物量回归模型^{[16, 17]}等方法, 实现各器官生物量模型与总生物量模型之间的相容性。此外, Parresol^[18]提出的非线性似乎不相关法, 能有效解决不同器官生物量方程的可加性问题。考虑到生物量模型形式、误差结构、可加性模型构造等因素对预测精度的影响^[19], 董利虎等^{[20, 21]}基于似然分析法和刀切法确定了生物量模型误差结构, 并采用似乎不相关回归方法对方程参数和偏差校正因子进行联合估计^[22], 建立了以对数转换为基础的可加性生物量方程系统。符利勇等^[6]和肖生苓等^[23]分别采用权函数、比例平差法、非线性似乎不相关回归法和非线性联立方程组法, 来消除方程的异方差和度量误差, 建立了兴安落叶松（Larix gmelinii）和马尾松（Pinus massoniana）总生物量与各器官的相容性生物量模型。此外, 还有学者采用混合模型和误差变量联立方程组方法^{[24, 25, 26]}, 构建了不同区域、不同起源立木生物量的通用性方程。

鉴于当前国内外有关生物量预测模型的研究主要集中在总生物量等于各器官生物量之和这一逻辑关系的探究, 常用建模方法主要有可加性生物量法、联立方程组方法、似乎不相关法、混合模型法等统计方法, 其中非线性似乎不相关法是估计各器官生物量的有效方法。然而基于非线性似乎不相关回归估计法, 在一个可加性生物量模型中, 同时估计出不同树种间各器官相容性的生物量模型参数及各器官分配模型的研究鲜为少见。因此, 本文以河北省塞罕坝机械林场华北落叶松（Larix principis-rupprechtii）人工林、油松（Pinus tabuliformis）人工林、白桦（Betula platyphylla）次生林为研究对象, 首先基于非线性似乎不相关回归估计法建立包含树种效应相容性生物量模型, 然后基于广义多项Logit模型建立不同树种各器官生物量分配模型, 为构建不同林分类型或起源的相容性生物量模型及其分配规律研究提供科学依据。

1 研究区概况

塞罕坝机械林场总场（41° 22′ ~42° 58′ N, 116° 53′ ~118° 31′ E）位于河北省最北部, 与内蒙古克什克腾旗和多伦县的部分地区接壤, 属阴山山脉与大兴安岭余脉的交接地带。林区属华北暖温带立地类型区域, 海拔1 010~1 940 m, 年均气温-1.2 ℃, 年均最高气温33.4 ℃, 年均最低气温-43.3 ℃; 年均日照时数2 548.7 h; 年均降水量约452.2 mm^[27]。研究区主要乔木树种有华北落叶松、白桦、云杉（Picea asperata）、樟子松（Pinus sylvestris var. mongolica）、山杨（Populus davidiana）、油松、蒙古栎（Quercus mongolica）等, 主要灌木树种有绣线菊（Spiraea salicifolia）、沙棘（Hippophae rhamnoides）、胡枝子（Lespedeza bicolor）、山刺玫（Rosa daverica）、稠李（Prunus padus）、华北忍冬（Lonicera tatarinowii）、大叶小檗（Berberis ferdinandi-coburgii）、栓翅卫矛（Euonymus phellomanus）等, 主要草本植物有蒲公英（Herba taraxaci）、野蔷薇（Rosa multiflora）、曼陀罗（Datura stramonium）、苔草（Carex tristachya）、草地老鹳草（Geanium daharicum）、藜芦（Veratrum nigrum）、地榆（Sanguisorba officinalis）、唐松草（Thalictrum aquilegifolium）等。

2 研究方法

2.1 数据来源

分别于2013— 2015年7— 8月在河北省塞罕坝机械林场, 共设置临时样地82块（其中华北落叶松人工林29块, 油松人工林26块, 白桦次生林27块）, 样地大小均为30 m× 30 m。按照传统经营方式, 对不同林分类型样地均已经营过2~4次, 其中, 华北落叶松、油松及白桦的地位指数分别在7.6~25.8、4.7~23.6、5.8~21.9 m范围内。观测样地立地因子（海拔、坡度、坡向等）并对样地内立木进行每木检尺。不同林分类型样地主要林分因子见表1。根据检尺结果在每块样地内分别选取1株平均木测定其生物量。树干生物量以1 m为一个区分段进行树干解析, 分别测定每个区分段的鲜重; 枝、叶生物量采用标准枝法, 按树冠长度将其平均分为上、中、下三层, 分别在每一层按树枝基径和长度选取标准枝, 测定标准枝鲜重及标准枝上所有叶鲜重, 用每层标准枝和枝条数量来计算枝、叶生物量; 树根生物量则采用全挖法, 根据直径大小将树根分为：小根（< 2 cm）、中根（2~5 cm）、大根（> 5 cm）3组分别称鲜重。然后在树干各区分段中间截取3~5 cm厚的圆盘, 称取鲜重并作为样品烘干, 其他各部分器官均取样1 000 g作为样品, 在85 ℃恒温下烘干至恒重, 根据器官样品鲜重和干重分别推算出样木各部分干重并汇总得到单木总干重。

表1 不同林分类型样地基本统计量 Table 1 Basic statistical information of sample sites of different forest types

2.2 生物量模型构建

树木生物量异速生长模型的基本形式可描述为 $Y = β_{0} X_{1}^{β_{1}} \dots X_{P}^{β_{P}} + ε$ , 考虑到模型中自变量个数, 通常把模型分为一元（胸径）^[21]、二元（胸径、树高）和多元（胸径、树高、冠幅、密度等）模型, 其中二元生物量模型预测效果最好且自变量容易观测^[25]。因此, 本文以二元生物量模型为基础模型进行研究。由于各器官生物量模型误差具有相关性, 利用非线性似乎不相关回归法进行参数估计要比普通最小二乘法更为准确^[22], 该方法不仅保证了各分量生物量方程的可加性（即生物量相容性）, 同时还考虑了各分量之间的相关性^[12], 模型表达式如式（1）所示。考虑到不同林分类型各器官对模型的影响, 并在一个模型中同时实现对不同树种各器官生物量模型参数同时进行估计, 在模型中构造一个哑变量I^[28], 即I=0为华北落叶松, I=-1为油松, I=1为白桦, 包含哑变量的不同树种可加性非线性似乎不相关模型可用式（2）表示, 研究由于样本数据较少, 故采用交叉验证方法^[22]对模型参数进行检验。

$\{\begin{array}{l} w_{gan} = a_{1} DB H^{a_{2}} H^{a_{3}} + ε \\ w_{zhi} = b_{1} DB H^{b_{2}} H^{b_{3}} + ε \\ w_{ye} = c_{1} DB H^{c_{2}} H^{c_{3}} + ε \\ w_{gen} = d_{1} DB H^{d_{2}} H^{d_{3}} + ε \\ w_{t} = w_{gan} + w_{zhi} + w_{ye} + w_{gen} + ε \end{array}$ （1）

$\{\begin{array}{l} w_{gan} = a_{11} DB H^{(a_{21} I_{1} + a_{22} I_{2} + a_{23} I_{3})} H^{(a_{31} I_{1} + a_{32} I_{2} + a_{33} I_{3})} + ε \\ w_{zhi} = b_{11} DB H^{(b_{21} I_{1} + b_{22} I_{2} + b_{23} I_{3})} H^{(b_{31} I_{1} + b_{32} I_{2} + b_{33} I_{3})} + ε \\ w_{ye} = c_{11} DB H^{(c_{21} I_{1} + c_{22} I_{2} + c_{23} I_{3})} H^{(c_{31} I_{1} + c_{32} I_{2} + c_{33} I_{3})} + ε \\ w_{gen} = d_{11} DB H^{(d_{21} I_{1} + d_{22} I_{2} + d_{23} I_{3})} H^{(d_{31} I_{1} + d_{32} I_{2} + d_{33} I_{3})} + ε \\ w_{guan} = w_{zhi} + w_{ye} + ε \\ w_{td} = w_{gan} + w_{zhi} + w_{ye} + ε \\ w_{t} = w_{gan} + w_{zhi} + w_{ye} + w_{gen} + ε \end{array}$ （2）

式中：W_gan、W_zhi、W_ye、W_gen、W_guan、W_td和W_t分别代表单木的树干、树枝、树叶、树根、树冠、地上及总生物量（kg/株）; DBH为胸径（cm）; H为树高（m）; a、b、c和d分别为模型参数; I₁、I₂、I₃为表示不同树种的哑变量; ε 为误差项。

2.3 生物量分配预测模型

在回归分析中, 若因变量是取值范围在(0, 1)区间的百分数时, 即因变量服从Beta分布^[12], 利用经典线性回归（普通最小二乘法和广义最小二乘法）进行预测研究时, 由于比例数据之间存在异方差^[15], 其预测值通常在(0, 1)区间之外, 预测效果较差。利用Beta分布回归模型对因变量为比例的数据进行建模, 能够克服以上问题且所产生的均方根误差和绝对偏差均较小。在林业相关研究中, 常运用Beta分布回归估计林冠郁闭度^[29]和灌木盖度^[30], Poudel等^[12]基于Beta分布回归建立了花旗松（Pseudotsuga menziesii）和美国黑松（Pinus contorta）不同器官生物量分配与预测模型。立木各器官生物量具有较大的相关关系^[15], 假设立木总生物量为1, 各器官分配比例在(0, 1)区间范围内, 并服从Beta分布, 其密度函数为：

$f (y; μ, ϕ) = \frac{Γ (ϕ)}{Γ (μϕ) Γ [(1 - μ) ϕ]} y^{μϕ - 1} {(1 - y)}^{(1 - μ) ϕ - 1}$ （3）

式中：y ~ Beta(0, 1); $ϕ$ > 0为尺度参数; μ 为平均参数, 0< μ < 1; Γ (.)为伽玛函数。因变量均值和方差可表示为：E(y)=μ , var(y)=[μ (1-μ )]/(1+ $ϕ$ )。假定y₁, y₂, …, y_n为随机样本, y_i ~ Beta(μ _i, $ϕ$ ), Beta回归模型可写成g(μ _i)=x_iβ =η _i, g(μ _i)为连接函数, x_i为p维变量, β 为回归系数。

多项Logit模型是在响应变量类别之间不存在序次关系时^[14], 基于最大似然估计法来预测各类别发生概率^[30], 多用于经济学领域概率估计, 在生态学领域应用较少。本研究基于Beta分布的广义多项Logit模型来建立单木水平各器官生物量分配比例模型, 保证器官生物量概率分布在(0, 1)区间内且各项之和为1, 不同器官生物量分配模型可用以下公式表示：

$p_{gan} = \frac{e^{a_{1} + a_{2} x}}{1 + e^{a_{1} + a_{2} x} + e^{b_{1} + b_{2} x} + e^{c_{1} + c_{2} x}}$ （4）

$p_{zhi} = \frac{e^{b_{1} + b_{2} x}}{1 + e^{a_{1} + a_{2} x} + e^{b_{1} + b_{2} x} + e^{c_{1} + c_{2} x}}$ （5）

$p_{ye} = \frac{e^{c_{1} + c_{2} x}}{1 + e^{a_{1} + a_{2} x} + e^{b_{1} + b_{2} x} + e^{c_{1} + c_{2} x}}$ （6）

$p_{gen} = \frac{1}{1 + e^{a_{1} + a_{2} x} + e^{b_{1} + b_{2} x} + e^{c_{1} + c_{2} x}}$ （7）

式中：p_gan、p_zhi、p_ye、p_gen分别为树干、树枝、树叶、树根的生物量占总生物量比例; a_i、b_i、c_i为模型参数; x为各器官生物量（kg/株）。

2.4 模型评价与精度检验

基于常见统计量, 对不同模型拟合精度和预测精度进行比较, 即确定系数（R²）、均方根误差（RMSE）、绝对误差（Bias）及赤池信息准则AIC指标, 对模型精度进行检验, 不同统计量计算公式如下：

$R^{2} = 1 - \overset{n}{\sum_{i = 1}} (y_{i} - {\hat{y}}_{i})^{2} / \overset{n}{\sum_{i = 1}} (y_{i} - {\overset{̅}{y}}_{i})^{2}$ （8）

$RMSE=\sqrt{\sum\limits^{n}_{i=1}(y_{i}-\hat{y}_{i})^{2}/(n-p)}$（9）

$Bias = \overset{n}{\sum_{i = 1}} (y_{i} - {\hat{y}}_{i}) / n$ （10）

$AIC = - 2 \log L + 2 p$ （11）

式中：y_i、 ${\hat{y}}_{i}$ 、 $\overset{̅}{y}$ 分别代表观测值、预测值和平均值; L为模型最大似然函数; n为样本数; p为模型中参数个数。

2.5 统计分析

数据处理及模型建立分别采用SPSS 21.0统计分析软件及SAS 9.2中PROC SORT、PROC LOGISTIC及PROC MODEL中似乎不相关过程完成, 文中图片均采用Origin 9.0完成。

3 结果与分析

3.1 似乎不相关生物量模型

基于包含哑变量的非线性似乎不相关方法, 建立了不同树种单木的各器官可加性生物量模型, 模型参数估计值、均方根误差、绝对误差及确定系数见表2。不同林分类型树干生物量模型拟合精度最高, 枝、叶、根生物量模型拟合精度稍低, 不同林分类型各器官生物量残差分布如图1所示。不同树种树干生物量模型的确定系数均大于0.90, 均方根误差和绝对误差分别在16.68~17.19 kg/株和0.84~1.07 kg/株的范围内; 枝、叶、根生物量模型确定系数在0.77~0.93范围内, 均方根误差和绝对误差分别在2.58~12.18 kg/株和0.83~1.39 kg/株的范围内。对预测值进行残差分析（图1）, 预测结果在[-95%, 95%]置信区间内, 预测值接近于真实值, 不同林分类型各器官生物量模型均能满足精度需求。

	Figure Option View Download New Window
	图1 不同林分类型各器官生物量残差分布Fig. 1 Residual distribution of biomass in various organs of different forest types

表2 不同林分类型生物量参数估计及统计检验 Table 2 Parameter estimation and goodness-of-fit statistics in biomass estimation of different forest types

3.2 生物量分配模型

树木各器官分配比例服从Beta分布, 基于广义多项Logit模型对不同树种各器官分配比例模型进行了拟合, 不同林分类型各器官生物量比例模型参数估计、参数标准误、信息准则（AIC值）如表3所示。经过似然比检验（Likelihood Ratio Test, LR）、比分检验（Score Test）和Wald检验对不同林分类型各器官比例模型进行检验, 不同林分类型各树种3种检验方法均达到显著水平（P< 0.001）, 不同器官各参数均表现为显著水平（P< 0.05）, 表明不同林分类型生物量分配比例模型拟合效果较好。

表3 不同林分类型各器官生物量比例模型参数估计与统计检验 Table 3 Parameter estimation and goodness-of-fit statistics of proportion model of organ biomass in different stand types

3.3 生物量分配格局

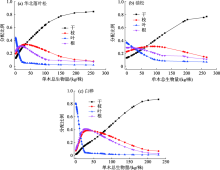
不同林分类型单木各器官生物量分配预测如图2所示, 其中华北落叶松人工林的干、枝、叶、根生物量分别占单木总生物量的0.13~0.81、0.19~0.07、0.45~0.05、0.23~0.07; 油松人工林的干、枝、叶、根生物量分别占单木总生物量的0.13~0.76、0.24~0.11、0.34~0.06、0.29~0.07; 白桦次生林干、枝、叶、根生物量分别占单木总生物量的0.02~0.87、0.08~0.07、0.81~0.02、0.09~0.04。随着单木生物量逐渐增加, 不同林分类型树干生物量比例稳定在0.76~0.87的范围内, 树枝生物量比例稳定在0.07~0.11的范围内, 树叶生物量比例稳定在0.02~0.07的范围内, 树根生物量比例稳定在0.04~0.07的范围内。

	Figure Option View Download New Window
	图2 不同林分类型各器官生物量分配规律Fig. 2 Distribution of biomass in various organs of different forest types

4 讨论

4.1 似乎不相关生物量模型

在生物量预测模型研究过程中, 解决不同树种各器官生物量相容性及其生物量分配规律一直是该领域的一个难题。研究中采用包含哑变量的非线性似乎不相关回归估计法, 建立了不同树种生物量预测模型, 该方法不仅考虑了单木总生物量与各器官生物量之间的内在相关性, 而且确保各器官生物量预测值之和等于总生物量, 其模型参数估计更有效^{[18, 22]}。将不同树种以哑变量方式加入到模型中, 同时将总生物量分为地上和地下（树根）两部分, 地上生物量分为树干和树冠两部分, 树冠生物量分为树枝和树叶两部分, 构建了包含哑变量的可加性生物量预测模型。通过分级控制建立单木总生物量模型, 能够有效消除度量误差, 解决生物量总量模型和各器官生物量模型不兼容的问题^[23]。考虑不同树种的相容性生物量模型, 研究中将树种作为哑变量来反映不同树种之间差异。符利勇等^[25]通过哑变量方法基于不同数量的自变量构建了相容性生物量模型, 曾伟生等^[26]利用线性混合效应模型实现了不同起源树种生物量模型通用性, 而非线性混合效应模型联立方程组法则缺乏相应的算法^[25]。Wang等^[31]研究表明选择哑变量方法和混合模型方法均可实现模型通用性且预测结果相同。因此, 与传统方法相比, 构建包含哑变量的非线性似乎不相关生物量预测模型既能保证模型预测精度, 又能实现预测模型通用性。

不同树种各器官生物量模型中, 树干预测模型拟合效果最好, 不同树种树干模型确定系数在0.94~0.97范围内, 均方根误差在16.68~17.19 kg/株范围内, 绝对误差在0.84~1.07 kg/株范围内; 而树枝、树叶、树根生物量模型拟合精度略低, 模型确定系数在0.77~0.93范围内, 均方根误差和绝对误差分别在2.58~12.18 kg/株和0.83~1.39 kg/株的范围内, 拟合结果仍能够满足预测要求。产生误差的原因可能是由于抽样误差、样本数量偏小、树种生长过程不同、林分结构差异及生物量分配等^{[12, 32]}影响, 导致数据变幅较大, 使部分器官产生了较大估计偏差。若想得到更精确的结果, 可能需在模型中加入立地条件、林分密度、不同发育阶段等能体现生物量差异的变量, 建立相应的指标权重体系^[14], 以实现对生物量较为精确的估测。

4.2 各器官生物量分配

树木各器官生物量直接反映光合产物积累量, 并影响最优化分配格局^[33]。不同树种各器官分配比例不同, 树干生物量比例为0.76~0.87, 树枝生物量比例为0.07~0.11, 树叶生物量比例为0.02~0.07, 树根生物量比例为0.04~0.07, 与部分学者^{[7, 13, 14, 17, 33]}研究结果相似。树木各器官生物量分配比例是动态变化的^[33], 通常会受到诸多生物学和非生物学因素限制, 如光照、水分、养分、年龄、密度及立木大小等^{[4, 34]}。在生长过程中, 林木会不断调节各器官生物量比例以最大化获得受限资源^{[35, 36]}。立木对光照、水分和养分竞争能力的高低是通过各器官生物量分配实现的^[37], 其中枝、叶、根生物量分配光照、水分和养分条件有显著相关性^[38], 当光照成为主要限制因子时, 立木将更多生物量分配给枝和叶, 以尽可能多的获取光照; 当水分或养分成为最主要的限制因子时, 更多生物量分配给根, 以获取更多土壤水分或养分^{[39, 40, 41]}。立木大小和密度导致树木间产生空间和资源竞争, 从而影响树木的可塑性, 进而导致各器官的生物量分配比例变化^{[42, 43]}。在无竞争存在时, 会增加地上各器官生物量分配^[17], 树干在立木组分中占有较大比重^[23], 但树干生物量分配比例在不同龄组间差异却非常显著^[7]。因此, 在今后研究立木各器官生物量分配过程中, 应与经营措施、立地类型、立木生长环境及不同发育阶段等结合起来并做进一步深入研究, 可能是全面理解树木异速生长机制的突破口。

致谢：感谢两名匿名审稿专家对本文提出了中肯的修改建议。

The authors have declared that no competing interests exist.

参考文献

文献顺序

[1]	PAN Y, BIRDSEY R A, PHILLIPS O L, et al. The structure, distribution, and biomass of the world’s forests[J]. Annual Review of Ecology, Evolution and Systematics, 2013, 44: 593-622. [本文引用:1]
[2]	陶冶, 张元明. 荒漠灌木生物量多尺度估测——以梭梭为例[J]. 草业学报, 2013, 22(6): 1-10. [TAO Y, ZHANG Y M. *Multi-scale biomass estimation of desert shrubs: A case study of Haloxylon ammodendron* in the Gurbantunggut Desert, China*. Acta Partaculturae Sinica*, 2013, 22(6): 1-10. ] [本文引用:1]
[3]	BROWM S L, SCHROEDER P, KEM J S. Spatial distribution of biomass in forests of the eastern USA[J]. Forest Ecology and Management, 1999, 123(1): 81-90. [本文引用:1]
[4]	MOKANY K, RAISON R J, PROKUSHKIN A. Critical analysis of root: Shoot ratios in terrestrial biomes[J]. Global Change Biology, 2006, 12(1): 84-96. [本文引用:3]
[5]	RIZVI R H, DHYANI S K, YADAV R S, et al. Biomass production and carbon stock of poplar agroforestry systems in Yamunanagar and Saharanpur districts of northwestern India[J]. Current Science, 2011, 100(5): 736-742. [本文引用:1]
[6]	符利勇, 雷渊才, 曾伟生. 几种相容性生物量模型及估计方法的比较[J]. 林业科学, 2014, 50(6): 42-54. [FU L Y, LEI Y C, ZENG W S. Comparison of several compatible biomass models and estimation approaches. Scientia Silvae Sinicae, 2014, 50(6): 42-54. ] [本文引用:2]
[7]	LI X, YI M J, SON Y, et al. *Biomass and carbon storage in an age-sequence of Korean pine ( Pinus koraiensis)* plantation forests in central Korea*[J]. Journal of Plant Biology*, 2011, 54(1): 33-42. [本文引用:3]
[8]	NVAR J. Biomass component equations for Latin American species and groups of species[J]. Annals of Forest Science, 2009, 66(2): 208-216. [本文引用:1]
[9]	ZIANIS D, MUUKKONEN P, MAKIPAA R, et al. Biomass and stem volume equations for tree species in Europe[J]. Silva Fennica Monographs, 2005, 4: 1-63. [本文引用:1]
[10]	黄兴召, 陈东升, 孙晓梅, 等. 基于异速参数概率分布的立木地上生物量估算[J]. 林业科学, 2014, 50(6): 34-41. [HUANG X S, CHEN D S, SUN X M, et al. Estimation of above-ground tree biomass based on probability distribution of allometric parameters. Scientia Silvae Sinicae, 2014, 50(6): 34-41. ] [本文引用:1]
[11]	罗永开, 方精云, 胡会峰. 山西芦芽山14种常见灌木生物量模型及生物量分配[J]. 植物生态学报, 2017, 41(1): 115-125. [LUO Y K, FANG J Y, HU H F. Biomass estimation models and allocation patterns of 14 shrub species in Mountain Luya, Shanxi, China. Chinese Journal of Plant Ecology, 2017, 41(1): 115-125. ] [本文引用:1]
[12]	POUDEL K P, TEMESGEN H. Methods for estimating aboveground biomass and its components for Douglas-fir and Lodgepole pine trees[J]. Canadian Journal of Forest Research, 2016, 46: 77-87. [本文引用:5]
[13]	汪珍川, 杜虎, 宋同清, 等. 广西主要树种(组)异速生长模型及森林生物量特征[J]. 生态学报, 2015, 35(13): 4462-4472. [WANG Z C, DU H, SONG T Q, et al. Allometric models of major tree species and forest biomass in Guangxi. Acta Ecologica Sinica, 2015, 35(13): 4462-4472. ] [本文引用:2]
[14]	付甜, 朱建华, 肖文发, 等. 八种亚热带森林类型乔木层地上生物量分配模型[J]. 林业科学, 2014, 50(9): 1-9. [FU T, ZHU J H, XIAO W F, et al. Above-ground biomass distribution models for arbor layer of eight subtropical forest types. Scientia Silvae Sinicae, 2014, 50(9): 1-9. ] [本文引用:5]
[15]	ZHAO D H, KANE M, MARKEWITZ D, et al. *Additive tree biomass equations for midrotation Loblolly pine* plantations*[J]. Forest Science*, 2015, 61(4): 613-623. [本文引用:3]
[16]	李海奎, 赵鹏祥, 雷渊才, 等. 基于森林清查资料的乔木林生物量估算方法的比较[J]. 林业科学, 2012, 48(5): 44-52. [LI H K, ZHAO P X, LEI Y C, et al. Comparison on estimation of wood biomass using forest inventory data. Scientia Silvae Sinicae, 2012, 48(5): 44-52. ] [本文引用:1]
[17]	李巍, 王传宽, 张全智. 林木分化对兴安落叶松异速生长方程和生物量分配的影响[J]. 生态学报, 2015, 35(6): 1679-1687. [LI W, WANG C K, ZHANG Q Z. *Differentiation of stand individuals impacts allometry and biomass allocation of Larix gmelinii* trees*. Acta Ecologica Sinica*, 2015, 35(6): 1679-1687. ] [本文引用:3]
[18]	PARRESOL B R. Additivity of nonlinear biomass equations[J]. Canadian Journal of Forest Research, 2001, 31(5): 865-878. [本文引用:2]
[19]	董利虎, 李凤日. 大兴安岭东部天然落叶松林可加性林分生物量估算模型[J]. 林业科学, 2016, 52(7): 13-21. [DONG L H, LI F R. Additive stand -level biomass models for natural larch forest in the east of Daxing’an Mountains. Scientia Silvae Sinicae, 2016, 52(7): 13-21. ] [本文引用:1]
[20]	董利虎, 李凤日. 三种林分生物量估算方法的比较[J]. 应用生态学报, 2016, 27(12): 3862-3870. [DONG L H, LI F R. Comparison of three stand -level biomass estimation methods. Chinese Journal of Applied Ecology, 2016, 27(12): 3862-3870. ] [本文引用:1]
[21]	董利虎, 张连军, 李凤日. 立木生物量模型的误差结构和可加性[J]. 林业科学, 2015, 51(2): 28-36. [DONG L H, ZHANG L J, LI F R. Error structure and additivity of individual tree biomass model. Scientia Silvae Sinicae, 2015, 51(2): 28-36. ] [本文引用:2]
[22]	BI H, TURNER J, LAMBERT M J. Additive biomass equations for native eucalypt forest trees of temperate Australia[J]. Trees, 2004, 18(4): 467-479. [本文引用:4]
[23]	肖生苓, 杨嘉龙. 大兴安岭北部兴安落叶松天然林单木地上生物量[J]. 林业科学, 2014, 50(8): 22-29. [XIAO S L, YANG J L. *Individual tree aboveground biomass of Larix gmelinii* natural forest in the northern Greater Khingan Mountains*. Scientia Silvae Sinicae*, 2014, 50(8): 22-29. ] [本文引用:3]
[24]	曾鸣, 聂祥永, 曾伟生. 中国杉木相容性立木材积和地上生物量方程[J]. 林业科学, 2013, 49(10): 74-79. [ZENG M, NIE X Y, ZENG W S. Compatible tree volume and aboveground biomass equations of Chinese fir in China. Scientia Silvae Sinicae, 2013, 49(10): 74-79. ] [本文引用:1]
[25]	符利勇, 唐守正, 张会儒, 等. 东北地区两个主要树种地上生物量通用方程构建[J]. 生态学报, 2015, 35(1): 150-157. [FU L Y, TANG S Z, ZHANG H R, et al. Generalized above-ground biomass equations for two main species in Northeast China. Acta Ecologica Sinica, 2015, 35(1): 150-157. ] [本文引用:4]
[26]	曾伟生, 唐守正, 夏忠胜, 等. 利用线性混合模型和哑变量模型方法建立贵州省通用性生物量方程[J]. 林业科学研究, 2011, 24(3): 285-291. [ZENG W S, TANG S Z, XIA Z S, et al. Using linear mixed model and dummy variable model approaches to construct generalized single-tree biomass equations in Guizhou. Forest Research, 2011, 24(3): 285-291. ] [本文引用:2]
[27]	王冬至, 张冬燕, 张志东, 等. 塞罕坝华北落叶松人工林断面积预测模型[J]. 北京林业大学学报, 2017, 39(7): 30-36. [WANG D Z, ZHANG D Y, ZHANG Z D, et al. *Prediction model for basal area of Larix principis-rupprechtii* plantation in Saihanba of Hebei Province, northern China*. Journal of Beijing Forestry University*, 2016, 52(1): 30-36. ] [本文引用:1]
[28]	SUZANNE M S, RUTISHAUSER E, CHAVE J, et al. Estimating the aboveground biomass in an old secondary forest on limestone in the Moluccas, indonesia: Comparing locally developed versus existing allometric models[J]. Forest Ecology and Management, 2017, 389: 27-34. [本文引用:1]
[29]	KORHONEN L, KORHONEN K T, STENBERG P, et al. Local models for forest canopy cover with beta regression[J]. Silva Fennica, 2007, 41(4): 671-685. [本文引用:1]
[30]	ESKELSON B N, MADSEN L, HAGAR J C, et al. Estimating riparian understory vegetation cover with beta regression and copula models[J]. Forest Science, 2011, 57: 212-221. [本文引用:2]
[31]	WANG T H, ZHOU D W, WANG P, et al. Size-dependent reproductive effort in amaranthus retroflexus: The influence of planting density and sowing data[J]. Canadian journal of botany, 2006, 84(3): 485-492. [本文引用:1]
[32]	董利虎, 李凤日, 宋玉文. 东北林区4 个天然针叶树种单木生物量模型误差结构及可加性模型[J]. 应用生态学报, 2015, 26(3): 704-714. [DONG L H, LI F R, SONG Y W. Error structure and additivity of individual tree biomass model for four natural conifer species in Northeast China. Chinese Journal of Applied Ecology, 2015, 26(3): 704-714. ] [本文引用:1]
[33]	巨文珍, 王新杰, 孙玉军. 长白落叶松林龄序列上的生物量及碳储量分配规律[J]. 生态学报, 2011, 31(4): 1139-1148. [JU W Z, WANG X J, SUN Y J. *Age structure effects on stand biomass and carbon storage distribution of Larix olgensis* plantation*. Acta Ecologica Sinica*, 2011, 31(4): 1139-1148. ] [本文引用:3]
[34]	黄从德, 张健, 杨万勤, 等. 四川省及重庆地区森林植被碳储量动态[J]. 生态学报, 2008, 28(3): 966-975. [HUANG C D, ZHANG J, YANG W Q, et al. Dynamics on forest carbon stock in Sichuan Province and Chongqing City. Acta Ecologica Sinica, 2008, 28(3): 966-975. ] [本文引用:1]
[35]	POORTER H, NIKLAS K J, REICH P B, et al. Biomass allocation to leaves, stems and roots: Meta-analyses of interspecific variation and environmental control[J]. The New Phytologist, 2012, 193(1): 30-50. [本文引用:1]
[36]	王平, 王天慧, 周道玮, 等. 植物地上竞争与地下竞争研究进展[J]. 生态学报, 2007, 27(8): 3489-3499. [WANG P, WANG T H, ZHOU D J, et al. A literature review on the above-and below-ground competition. Acta Ecologica Sinica, 2007, 27(8): 3489-3499. ] [本文引用:1]
[37]	黎磊, 周道玮, 盛连喜. 植物种群自疏过程中构件生物量与密度的关系[J]. 生态学报, 2012, 32(13): 3987-3997. [LI L, ZHOU D W, SHENG L X. Allometric relationship between mean component biomass and density during the course of self-thinning for fagopyrum esculentum populations. Acta Ecologica Sinica, 2012, 32(13): 3987-3997. ] [本文引用:1]
[38]	SHIPLEY B, MEZIANE D. The balanced-growth hypothesis and the allometry of leaf and root biomass allocation[J]. Functional Ecology, 2002, 16(3): 326-331. [本文引用:1]
[39]	OSONE Y, TATENO M. Applicability and limitations of optimal biomass allocation models: A test of two species from fertile and infertile habitats[J]. Annals of Botany, 2005, 95(7): 1211-1220. [本文引用:1]
[40]	仇瑶, 常顺利, 张毓涛, 等. 天山林区六种灌木生物量的建模及其器官分配的适应性[J]. 生态学报, 2015, 35(23): 7842-7851. [QIU Y, CHANG S L, ZHANG Y T, et al. Biomass estimation modeling and adaptability analysis of organ allocation in six common shrub species in Tianshan Mountains forests, China. Acta Ecologica Sinica, 2015, 35(23): 7842-7851. ] [本文引用:1]
[41]	朱桂丽, 李杰, 魏学红, 等. 青藏高寒草地植被生产力与生物多样性的经度格局[J]. 自然资源学报, 2017, 32(2): 210-222. [ZHU G L, LI J, WEI X H, et al. Longitudinal patterns of productivity and plant diversity in Tibetan alpine grassland s. Journal of Natural Resources, 2017, 32(2): 210-222. ] [本文引用:1]
[42]	安慧, 上官周平. 密度对刺槐幼苗生物量及异速生长模式的影响[J]. 林业科学, 2008, 44(3): 151-155. [AN H, SHANGGUAN Z P. *Effects of density on biomass and allometric pattern of Robinia pseudoacacia* seedling*. Scientia Silvae Sinicae*, 2008, 44(3): 151-155. ] [本文引用:1]
[43]	黄迎新, 赵学勇, 张洪轩, 等. 沙米表型可塑性对土壤养分、水分和种群密度变化的响应[J]. 应用生态学报, 2008, 19(12): 2593-2598. [HUANG Y X, ZHAO X Y, ZHANG H X, et al. Responses of agriophyllum squarrosum phenotypic plasticity to the changes of soil nutrient and moisture content sand population density. Chinese Journal of Applied Ecology, 2008, 19(12): 2593-2598. ] [本文引用:1]

2013

0.0

... 森林生物量在研究森林生态系统结构与功能^[1]、生产力和生产潜力评价^[2]、物质循环和能量流动^[3,4]、碳循环和气候变化影响与适应^[5]中具有重要意义 ...

2013

0.0

陶冶, 张元明. 荒漠灌木生物量多尺度估测——以梭梭为例[J]. 草业学报, 2013, 22(6): 1-10.

[TAO

, ZHANG Y

. Multi-scale biomass estimation of desert shrubs: A case study of Haloxylon ammodendron in the Gurbantunggut Desert, China. Acta Partaculturae Sinica, 2013, 22(6): 1-10. ]

灌木是荒漠生态系统重要的组成部分，其生物量估算与分配特征是研究荒漠生态系统结构、功能、物质和能量流动的重要指标。但目前关于荒漠灌木生物量的研究仍较缺乏。破坏性的生物量估测方法不适宜在生态系统脆弱的荒漠地区大面积使用，因此通过模型法对灌木生物量进行多尺度估测具有重要意义。本研究以准噶尔荒漠生态系统建群种———梭梭为例，选择多种植物外部形态特征参数，利用相关生长模型（幂函数），分别在单株、样方及区域尺度对梭梭的地上（ AGB ）和地下生物量（ BGB ）进行建模和估算。结果表明，以植冠体积（ CH ）为指标的估测模型（ AGB ＝０．３６２８× CH ０．９６０５）能较好地反映梭梭单株地上生物量累计特征，而单株地下生物量可通过模型 BGB ＝０．８７３７× AGB ０．９３９４得到。样方内梭梭总冠幅面积（ＴＣ）是估测样方（０．１ｈｍ２）总生物量（ TAGB ＝０．６７５７× TC １．１３４３， TBGB ＝０．６３８４× TC １．０９５９）的有效参数。在大尺度上（区域），利用梭梭相对盖度（ＲＣ）估测其生物量密度（ DAGB ＝０．０９２１× RC １．１３４３， DBGB ＝０．０７９６× RC １．０９５９）具有良好效果，进而结合区域面积得到梭梭总生物量。研究表明，相对盖度的方法从生物量密度的角度解决了尺度转换问题，使用时没有尺度限制。未来还可以通过航拍、遥感等手段快速获取相关区域梭梭群落相对盖度，结合上述模型准确估测其地上、地下生物量。

1999

0.0

2006

0.0

... 然而不同器官生物量及分配规律通常会受到自然因素（光合作用、呼吸作用、枯损与生长等）和人为因素（采伐、修枝等）的影响^[4],因此,世界各国越来越重视对森林生物量的估计、监测和评价^[6],其中生物量建模是项重要基础工作 ...

... 树木各器官生物量分配比例是动态变化的^[33],通常会受到诸多生物学和非生物学因素限制,如光照、水分、养分、年龄、密度及立木大小等^[4,34] ...

2011

0.0

2014

0.0

符利勇, 雷渊才, 曾伟生. 几种相容性生物量模型及估计方法的比较[J]. 林业科学, 2014, 50(6): 42-54.

[FU L

, LEI Y

, ZENG W

. Comparison of several compatible biomass models and estimation approaches. Scientia Silvae Sinicae, 2014, 50(6): 42-54. ]

So far, the approaches of nonlinear seemingly unrelated regression (NSUR), nonlinear adjustment in proportion (NAP) and nonlinear simultaneous equations (NSE) have been proposed to establish compatible biomass models. However, to our knowledge, systemic comparison of these methods is not studied. Therefore, the three methods NSUR, NAP and NSE were compared based on predictive accuracy using 150 masson pine ( Pinus massoniana ) biomass data in this study. Two alternative approaches, controlling jointly from level to level by ratio functions and controlling directly under total biomass by proportion functions were considered for the two approaches of NAP and NSE. Six candidate tree variables of diameter at breast height, tree height, ground diameter, age, under branch height and crown width were evaluated for their contribution to biomass models improvement. Single variable, bivariate and multivariate (three variables) biomass models were established based on the first three of the most significant tree characteristics. Heteroskedasticity in the biomass models was removed by weighted least square regression. Compatible biomass models were established and estimated based on single variable, bivariate and multivariate using NSUR, NAP and NSE. The results showed that the three analyzed methods could ensure efficiently that components of biomass added up to the total biomass with high prediction accuracy. However, overall, NSE had the highest prediction accuracy and most stable, following by NSUR, and NAP was the worst. For balancing the model prediction accuracy and survey cost, the NSE of controlling directly under total biomass with diameter at breast height and height as stand variables was proposed to construct compatible biomass model at considering or no considering stand origin situation based on the systemic comparison of modelling and validation data sets.

以南方150株马尾松地上生物量数据为例，在考虑林分起源和未考虑林分起源2种情形下，对非线性似然无关回归法、比例平差法和非线性联立方程组法3种方法进行综合比较研究。根据分配层次不同，比例平差法和非线性联立方程组法将进一步考虑总量直接控制和分级联合控制2种方案。从直径、树高、地径、年龄、枝下高和冠幅6个林分变量中选取不同的变量构建一元、二元和三元生物量模型，利用加权最小二乘回归法消除生物量模型中存在的异方差性。基于独立形式的一元、二元和三元模型，利用非线性似然无关回归法、比例平差法和非线性联立方程组法构建相应的相容性生物量模型。结果表明：在考虑和未考虑林分起源情形下，3种估计方法都能有效保证各分量生物量总和等于总生物量，预测精度较高。总体而言，非线性联立方程组法预测精度更高、稳定性更强，其次是非线性似然无关回归法，最差的是非线性比例平差法；根据建模数据和检验数据综合比较得知，在考虑和未考虑林分起源情形下，总量控制联立方程组法对应的二元相容性生物量模型预测精度最高。

... 符利勇等^[6]和肖生苓等^[23]分别采用权函数、比例平差法、非线性似乎不相关回归法和非线性联立方程组法,来消除方程的异方差和度量误差,建立了兴安落叶松（Larix gmelinii）和马尾松（Pinus massoniana）总生物量与各器官的相容性生物量模型 ...

2011

0.0

... 在树木生长过程中,各器官生物量生长均呈现异速生长规律^[7],并在生态学和应用环境学研究中广泛应用^[8,9,10] ...

... 07,与部分学者^{[7,13,14,17,33]}研究结果相似 ...

... 在无竞争存在时,会增加地上各器官生物量分配^[17],树干在立木组分中占有较大比重^[23],但树干生物量分配比例在不同龄组间差异却非常显著^[7] ...

2009

0.0

... 在树木生长过程中,各器官生物量生长均呈现异速生长规律^[7],并在生态学和应用环境学研究中广泛应用^[8,9,10] ...

2005

0.0

... 在树木生长过程中,各器官生物量生长均呈现异速生长规律^[7],并在生态学和应用环境学研究中广泛应用^[8,9,10] ...

2014

0.0

黄兴召, 陈东升, 孙晓梅, 等. 基于异速参数概率分布的立木地上生物量估算[J]. 林业科学, 2014, 50(6): 34-41.

[HUANG X

, CHEN D

, SUN X

, et al. Estimation of above-ground tree biomass based on probability distribution of allometric parameters. Scientia Silvae Sinicae, 2014, 50(6): 34-41. ]

Allometric biomass equations are widely used to predict above-ground biomass in forest ecosystems. It found the distribution of the parameters a and b of the allometry between above-ground biomass ( M ) and diameter at breast height( D ), ln M = a + b ln D , well approximated by a bivariate normal from analysis a data of 304 functions of 80 papers. ANOVA was tested to parameters in seven genera. In contrast to the parameter a , there was significant difference in parameter b . There were negative correlation between the parameter a and b , the parameter b and latitude. From this negative correlation, simultaneous-equation was used to build general model for parameters which were changed by latitude. Three methods which include established general model, minimum-least-square regression and Bayesian approach were used to fitting the above-ground biomass of Larix kaempferi in sub-tropical alpine area. The result showed that general model was the lowest precise quantifications( R 2 =0.892), but it could estimate the biomass where forest situated in latitude without samples. With sample size was more than 50, both Bayesian method and minimum-least-square regression was no significant difference in the mean absolute error. And it was less than 50, Bayesian method was better than minimum-least-square regression. Therefore, it was suggested that Bayesian method was used to estimate above-ground biomass when the sample size was less than 50.

对收集的80篇文献中304个地上部分生物量（ M ）和胸径（ D ）的异速生物量模型ln M = a + b ln D 数据集研究发现：模型参数 a 和 b 符合二元正态分布；参数 a 和 b 之间、参数 b 和纬度间呈负相关，并依此相关关系应用联立方程组建立参数 a 和 b 随纬度变化的通用模型。以实测的北亚热带高山区日本落叶松地上部分生物量数据对新建的通用模型、最小二乘法和贝叶斯方法拟合生物量的适用性进行研究，结果表明：虽然通用模型的拟合精度最低（ R 2 为0.892），但可以根据植物生长的纬度实现无实测样地情况下的生物量估算。在拟合样本≥50时，最小二乘法和贝叶斯方法的拟合效果无显著差异；当拟合样本<50时，贝叶斯方法的拟合效果优于最小二乘法。因此在建模样本<50时，建议使用贝叶斯方法估测立木地上部分生物量。

... 在树木生长过程中,各器官生物量生长均呈现异速生长规律^[7],并在生态学和应用环境学研究中广泛应用^[8,9,10] ...

2017

0.0

罗永开, 方精云, 胡会峰. 山西芦芽山14种常见灌木生物量模型及生物量分配[J]. 植物生态学报, 2017, 41(1): 115-125.

[LUO Y

, FANG J

, HU H

. Biomass estimation models and allocation patterns of 14 shrub species in Mountain Luya, Shanxi, China. Chinese Journal of Plant Ecology, 2017, 41(1): 115-125. ]

... 不同器官生物量与分配是表征立木生长过程的重要指标^[11],对了解树木变异、预测林火、木材生产及养分循环等^[12]具有重要作用,因此对立木不同器官生物量估计及其分配的研究是必须的 ...

2016

0.0

... 由于各器官生物量模型误差具有相关性,利用非线性似乎不相关回归法进行参数估计要比普通最小二乘法更为准确^[22],该方法不仅保证了各分量生物量方程的可加性（即生物量相容性）,同时还考虑了各分量之间的相关性^[12],模型表达式如式（1）所示 ...

... 3 生物量分配预测模型在回归分析中,若因变量是取值范围在(0, 1)区间的百分数时,即因变量服从Beta分布^[12],利用经典线性回归（普通最小二乘法和广义最小二乘法）进行预测研究时,由于比例数据之间存在异方差^[15],其预测值通常在(0, 1)区间之外,预测效果较差 ...

... 在林业相关研究中,常运用Beta分布回归估计林冠郁闭度^[29]和灌木盖度^[30],Poudel等^[12]基于Beta分布回归建立了花旗松（Pseudotsuga menziesii）和美国黑松（Pinus contorta）不同器官生物量分配与预测模型 ...

... 产生误差的原因可能是由于抽样误差、样本数量偏小、树种生长过程不同、林分结构差异及生物量分配等^[12,32]影响,导致数据变幅较大,使部分器官产生了较大估计偏差 ...

2015

0.0

汪珍川, 杜虎, 宋同清, 等. 广西主要树种(组)异速生长模型及森林生物量特征[J]. 生态学报, 2015, 35(13): 4462-4472.

[WANG Z

, DU

, SONG T

, et al. Allometric models of major tree species and forest biomass in Guangxi. Acta Ecologica Sinica, 2015, 35(13): 4462-4472. ]

... 目前国内外学者已对生物量建模工作做了部分研究,汪珍川等^[13]、付甜等^[14]基于幂函数模型构建了亚热带主要森林类型地上各器官生物量模型 ...

... 07,与部分学者^{[7,13,14,17,33]}研究结果相似 ...

2014

0.0

付甜, 朱建华, 肖文发, 等. 八种亚热带森林类型乔木层地上生物量分配模型[J]. 林业科学, 2014, 50(9): 1-9.

[FU

, ZHU J

, XIAO W

, et al. Above-ground biomass distribution models for arbor layer of eight subtropical forest types. Scientia Silvae Sinicae, 2014, 50(9): 1-9. ]

In this study, the volume-to-biomass conversion models and the proportion models for biomass components of 8 subtropical forest types in China were established by using the power function model and multinomial logit model, respectively. The results show that the fitting results of the volume-to-biomass conversion models for every forest type except the evergreen broad-leaved forest exhibit significant relations ( R 2 >0.5, P -2 . The testing accuracy is between 31.14%-91.79%, which are all above 70% except for evergreen broad-leaved forest. On the other hand, the fitting results of proportion models for the biomass components reach significant level ( P <0.05) except for the evergreen broad-leaved forest, and the predicting residuals decrease with the increased independent variable value. The root mean square errors of stem, bark, branch and leaf biomass proportion of total tree biomass are all less than 0.1, that is 0.031~0.085, 0.005~0.041, 0.029~0.103 and 0.016~0.083. The prediction accuracy reaches 91.04%~96.14%, 62.71%~94.48%, 63.70%~94.47%, and －8.86%~83.92%, respectively. The volume-to-biomass conversion models and the proportion models for biomass components in this paper are reasonable models for the 8 subtropical forest types except for the evergreen broad-leaved forest, and the obtained model parameters also can provide a reference for studying biomass distribution of the other subtropical forests

以我国亚热带的8种森林类型的乔木层为研究对象,采用幂函数模型和多项logit模型分别构建各森林类型的材积-生物量转换模型和林木器官生物量比例模型。结果表明: 材积-生物量转换模型的拟合结果表现为除常绿阔叶林外,其他森林类型的材积与生物量均显著相关( R 2 >0.5, P -2 ,抽样精度检验结果显示,材积-生物量转换模型的预测精度为31.14%~91.79%,除常绿阔叶林以外,其他森林类型的模型预测精度均达到70%以上；林木器官生物量比例模型的拟合结果表现为除常绿阔叶林外实测值与预测值的相关性均显著( P <0.05),预测残差随自变量的增大而减小；干、皮、枝和叶生物量比例模型的均方根误差均不超过0.1,分别为0.031~0.085,0.005~0.041,0.029~0.103和0.016~0.083,各林木器官比例的预测精度分别达到91.04%~96.14%,62.71%~94.48%,63.70%~94.47%和-8.86%~83.92%；各森林类型(除常绿阔叶林外)的乔木层地上材积-生物量模型和林木器官生物量比例模型的可行性较高,所得模型参数也可为亚热带森林生物量分配研究提供参考.

... 目前国内外学者已对生物量建模工作做了部分研究,汪珍川等^[13]、付甜等^[14]基于幂函数模型构建了亚热带主要森林类型地上各器官生物量模型 ...

... 然而由各器官生物量之和估计总生物量时预测误差较大^[14,15] ...

... 多项Logit模型是在响应变量类别之间不存在序次关系时^[14],基于最大似然估计法来预测各类别发生概率^[30],多用于经济学领域概率估计,在生态学领域应用较少 ...

... 若想得到更精确的结果,可能需在模型中加入立地条件、林分密度、不同发育阶段等能体现生物量差异的变量,建立相应的指标权重体系^[14],以实现对生物量较为精确的估测 ...

... 07,与部分学者^{[7,13,14,17,33]}研究结果相似 ...

2015

0.0

... 然而由各器官生物量之和估计总生物量时预测误差较大^[14,15] ...

... 立木各器官生物量具有较大的相关关系^[15],假设立木总生物量为1,各器官分配比例在(0, 1)区间范围内,并服从Beta分布,其密度函数为： ...

2012

0.0

李海奎, 赵鹏祥, 雷渊才, 等. 基于森林清查资料的乔木林生物量估算方法的比较[J]. 林业科学, 2012, 48(5): 44-52.

[LI H

, ZHAO P

, LEI Y

, et al. Comparison on estimation of wood biomass using forest inventory data. Scientia Silvae Sinicae, 2012, 48(5): 44-52. ]

... 常用度量误差法、转换因子连续函数法和加权生物量回归模型^[16,17]等方法,实现各器官生物量模型与总生物量模型之间的相容性 ...

2015

0.0

李巍, 王传宽, 张全智. 林木分化对兴安落叶松异速生长方程和生物量分配的影响[J]. 生态学报, 2015, 35(6): 1679-1687.

[LI

, WANG C

, ZHANG Q

. Differentiation of stand individuals impacts allometry and biomass allocation of Larix gmelinii trees. Acta Ecologica Sinica, 2015, 35(6): 1679-1687. ]

Differentiation of stand individuals results from the competition of limited resources and thus affects allometry and allocation of tree biomass, but the extent to its impact has rarely been quantified. In this study, 38 Larix gmelinii trees, including 15 dominant, 16 intermediate, and 7 suppressed trees that were classified using a relative diameter method, were harvested for quantifying the effect of tree differentiation in the stand on the allometry and allocation of biomass. The results showed that the diameter at crown base was the most reliable predictor for branch and foliage biomass, whereas the diameter at breast height (DBH) was the best predictor for the other biomass components. For a specific value within a certain range of the DBH, the allometric models for belowground biomass components did not differ significantly among the tree differentiation classes ( P > 0.05). However, the dominant trees allocated more biomass to branch and foliage components, whereas the intermediate trees allocated more biomass to stem component than the dominant, and more biomass to aboveground component than the suppressed. The tree height of the suppressed and intermediate trees was significantly greater than the dominant for a given DBH. The proportions of all the components except for stump to the total biomass did not differ significantly ( P > 0.05) among the tree differentiation classes. The root shoot ratio was relatively constant for all the tree-differentiation classes. These results suggest that the differentiation of stand individuals in the larch trees mainly caused by resource competition diverts the allometry and allocation of the aboveground biomass components, but the relative allocation pattern is conservative.

林木因对资源竞争而产生分化,从而影响林木的异速生长方程和生物量分配,但其影响程度还不清楚。采用林木相对直径法将38株兴安落叶松( Larix gmelinii )样木在林分中的分化等级分为优势木、中等木和被压木,量化林木分化对林木异速生长方程和生物量分配的影响。结果显示:生物量组分异速生长方程多以胸径(DBH)为自变量为好,但以枝下高处的树干直径为自变量估测其枝、叶生物量时更精确。在一定的胸径范围内,同一胸径下不同林木分化等级的地下部分各组分生物量没有显著差异( P > 0.05),但优势木分配更多的生物量给枝和叶,中等木比优势木分配更多的生物量给树干,中等木比被压木分配更多的生物量给地上部分,而且被压木和中等木的树高显著高于优势木。除根茎生物量之外,不同林木分化等级的生物量组分(包括枝、叶、树干和根系)的相对分配比例无显著差异( P > 0.05),根冠比保持相对稳定。这些结果表明,主要由竞争而引起的林木分化改变了兴安落叶松地上生物量组分的异速生长和分配,但其相对分配格局较为保守。

... 常用度量误差法、转换因子连续函数法和加权生物量回归模型^[16,17]等方法,实现各器官生物量模型与总生物量模型之间的相容性 ...

... 07,与部分学者^{[7,13,14,17,33]}研究结果相似 ...

... 在无竞争存在时,会增加地上各器官生物量分配^[17],树干在立木组分中占有较大比重^[23],但树干生物量分配比例在不同龄组间差异却非常显著^[7] ...

2001

0.0

... 此外,Parresol^[18]提出的非线性似乎不相关法,能有效解决不同器官生物量方程的可加性问题 ...

... 研究中采用包含哑变量的非线性似乎不相关回归估计法,建立了不同树种生物量预测模型,该方法不仅考虑了单木总生物量与各器官生物量之间的内在相关性,而且确保各器官生物量预测值之和等于总生物量,其模型参数估计更有效^[18,22] ...

2016

0.0

董利虎, 李凤日. 大兴安岭东部天然落叶松林可加性林分生物量估算模型[J]. 林业科学, 2016, 52(7): 13-21.

[DONG L

, LI F

. Additive stand -level biomass models for natural larch forest in the east of Daxing’an Mountains. Scientia Silvae Sinicae, 2016, 52(7): 13-21. ]

... 考虑到生物量模型形式、误差结构、可加性模型构造等因素对预测精度的影响^[19],董利虎等^[20,21]基于似然分析法和刀切法确定了生物量模型误差结构,并采用似乎不相关回归方法对方程参数和偏差校正因子进行联合估计^[22],建立了以对数转换为基础的可加性生物量方程系统 ...

2016

0.0

董利虎, 李凤日. 三种林分生物量估算方法的比较[J]. 应用生态学报, 2016, 27(12): 3862-3870.

[DONG L

, LI F

. Comparison of three stand -level biomass estimation methods. Chinese Journal of Applied Ecology, 2016, 27(12): 3862-3870. ]

At present, the forest biomass methods of regional scale attract most of attention of the researchers, and developing the stand-level biomass model is popular. Based on the forestry inventory data of larch plantation ( Larix olgensis ) in Jilin Province, we used nonlinear seemly unrelated regression (NSUR) to estimate the parameters in two additive system of standlevel biomass equations,  i.e ., standlevel biomass equations including the stand variables and stand biomass equations including the biomass expansion factor ( i.e ., Model system Ⅰ and Model system Ⅱ), listed the constant biomass expansion factor for larch plantation and compared the prediction accuracy of three standlevel biomass estimation methods. The results indicated that for two additive system of biomass equations, the adjusted coefficient of determination ( R a 2 ) of the total and stem equations was more than 0.95, the root mean squared error (RMSE), the mean prediction error (MPE) and the mean absolute error (MAE) were smaller. The branch and foliage biomass equations were worse than total and stem biomass equations, and the adjusted coefficient of determination ( R a 2 ) was less than 0.95. The prediction accuracy of a constant biomass expansion factor was relatively lower than the prediction accuracy of Model system Ⅰ and Model system Ⅱ. Overall, although standlevel biomass equation including the biomass expansion factor belonged to the volumederived biomass estimation method, and was different from the stand biomass equations including stand variables in essence, but the obtained prediction accuracy of the two methods was similar. The constant biomass expansion factor had the lower prediction accuracy, and was inappropriate. In addition, in order to make the model parameter estimation more effective, the established standlevel biomass equations should consider the additivity in a system of all tree component biomass and total biomass equations.

区域森林生物量的估算方法是人们目前关注的焦点,建立林分生物量模型成为一种趋势.本文以吉林省落叶松人工林固定样地为例,采用非线性似乎不相关回归法构建2种林分生物量模型,即基于林分变量的林分生物量模型(模型系统Ⅰ)和基于生物量换算系数的林分生物量模型(模型系统Ⅱ),给出落叶松人工林固定生物量换算系数值,并比较了3种林分生物量估算方法的预估精度.结果表明: 所建立的2种林分生物量模型中,总生物量和树干生物量模型拟合和预测效果较好,其 R a 2 >0.95,且均方根误差(RMSE)、平均预测误差(MPE)和平均绝对误差(MAE)都较小.树叶和树枝生物量模型拟合和预测效果相对较差,其模型的 R a 2

2015

0.0

董利虎, 张连军, 李凤日. 立木生物量模型的误差结构和可加性[J]. 林业科学, 2015, 51(2): 28-36.

[DONG L

, ZHANG L

, LI F

. Error structure and additivity of individual tree biomass model. Scientia Silvae Sinicae, 2015, 51(2): 28-36. ]

【Objective】Forest biomass is a basic quantity character of the forest ecological system. Biomass data are the foundation of researching many forestry and ecology problems. Therefore, accurate quantification of biomass is critical for calculating carbon storage, as well as for studying climate change, forest health, forest productivity and nutrient cycling, etc. Directly measuring the actual weight of each component (i.e., stem, branch, foliage and root) is undoubtedly the most accurate method, but it is destructive, time consuming, and costly. Thus, developing biomass models is regarded as a better approach to estimating forest biomass. However, some issues are needed to take care when constructing and applying biomass models, such as: 1) some reported biomass models may not hold the additivity or compatibility among tree component models; 2) which model error structure is appropriate for biomass data, i.e., additive error structure versus multiplicative error structure; 3) few models are available for tree belowground (root) biomass. Researchers have been continuously working and debating on these issues over the last decades. Development of the additive system of biomass equations were reported in the literature. However, how to evaluate the model error structure of the biomass equation in forestry have not been well investigated so far. The present paper mainly deals with two parts: evaluating error structure of the biomass model and developing the additive system of biomass equations.【Method】The P. simonii×P. nigra plantation in the west of Heilongjiang Province of China is selected to ensure error structure by likelihood analysis. Nonlinear seemly unrelated regression (NSUR) of SAS/ETS module is used to estimate the parameters in the additive system of biomass equations. The biomass model validation is accomplished by Jackknifing technique.【Result】The multiplicative error structure was favored for the total and component biomass equations for P. simonii × P. nigra plantation by a likelihood analysis, and the additive system of log-transformed biomass equations should be applied. Overall, the R a 2 of all biomass models was between 0.92 and 0.99. The mean relative error and mean absolute relative error were smaller for most biomass models. All models for total and component biomass had the good prediction precision (85 % or more). The effect of total tree, aboveground and stem biomass models are better than root, branch, foliage and crown biomass models. Overall, all models for total and component biomass could be a good predict of the P. simonii × P. nigra biomass.【Conclusion】Although the significance of likelihood analysis is proposed by several studies, it has not been widely applied in forestry. When total biomass is divided into aboveground and belowground biomass, aboveround biomass is divided into stem and crown biomass, crown biomass is divided into branch and foliage biomass, and stem biomass is divided into bark and wood biomass, the additivity of total and component biomass should be taken into account. Overall, the error structure and additivity of biomass models are the two key issues, and should be taken into account when biomass models are constructed. If the two issues are well solved, the constructed biomass models will be more effective.

【目的】从确定生物量模型误差结构和建立可加性生物量模型2方面进行立木生物量研究,为构建生物量模型提供建议。【方法】以黑龙江西部平原地区人工林小黑杨为例,利用似然分析法判断总生物量及各分项生物量模型的误差结构,在此基础上利用SAS/ETS模块的非线性似乎不相关回归建立其可加性生物量模型,并采用"刀切法"对生物量模型进行评价。【结果】经似然分析法判断,人工林小黑杨生物量模型的误差结构都为相乘的,对数转换的可加性生物量模型应当被选用。所建立的人工林小黑杨可加性生物量模型的调整后确定系数 R a 2 为0.92~0.99,绝大多数模型的平均相对误差以及平均相对误差绝对值都较小,所有模型的预测精度都在85%以上,且总生物量、地上和树干生物量模型效果较好,树根、树枝、树叶和树冠生物量模型效果较差。总的来说,各分项生物量和总生物量模型的拟合效果和预测能力较好。【结论】模型的误差结构和可加性是构建生物量模型中所存在的2个关键问题,建议在构建生物量模型时考虑并解决这2个问题。

... 2 生物量模型构建树木生物量异速生长模型的基本形式可描述为 Y=β0X1β1⋯XPβP+ε,考虑到模型中自变量个数,通常把模型分为一元（胸径）^[21]、二元（胸径、树高）和多元（胸径、树高、冠幅、密度等）模型,其中二元生物量模型预测效果最好且自变量容易观测^[25] ...

2004

0.0

... 考虑到不同林分类型各器官对模型的影响,并在一个模型中同时实现对不同树种各器官生物量模型参数同时进行估计,在模型中构造一个哑变量I^[28],即I=0为华北落叶松,I=-1为油松,I=1为白桦,包含哑变量的不同树种可加性非线性似乎不相关模型可用式（2）表示,研究由于样本数据较少,故采用交叉验证方法^[22]对模型参数进行检验 ...

2014

0.0

肖生苓, 杨嘉龙. 大兴安岭北部兴安落叶松天然林单木地上生物量[J]. 林业科学, 2014, 50(8): 22-29.

[XIAO S

, YANG J

. Individual tree aboveground biomass of Larix gmelinii natural forest in the northern Greater Khingan Mountains. Scientia Silvae Sinicae, 2014, 50(8): 22-29. ]

Based on 104 sample tree trunk and branches parse biomass data in 19 sample plots, established the compatible model of aboveground total model and component of Larix gmelinii natural forest, by using weight function and simultaneous linear equations to eliminate heteroscedasticity and measurement error equation. The results showed that: 1) Compatibility biomass model solved the total biomass model and component biomass model of incompatible problem, and the compatibility of biomass model prediction accuracy was higher than empirical model; 2) Utilize modern built biomass model parameter determination coefficient R 2 and compatibility model deviation statistics estimate the standard deviation SEE, mean estimated error MPE, mean relative deviation ME, mean relative deviation absolute MAE were 0.907-0.947,1.887-17.368,1.011%-2.703%,-4.937%-6.998%,5.408%-10.886%; 3) Statistical analysis of the measured values of Larix gmelinii natural forest in the northern Greater Khingan Mountains, got the region single natural forest stem biomass covered the aboveground biomass of 60.37%-76.80%, stem biomass proportion with the increase of forest age increased first, then decreased. Bark biomass covered the aboveground biomass of 7.15%-20.11%, the proportion trend of decrease with the increase of forest age. Branch biomass covered the aboveground biomass of 8.51%-14.29%, branch biomass proportion along with the age increasing basic rendering. Leaf biomass covered the aboveground biomass of 5.12%-7.09%,leaf biomass accounted for the proportion of the biggest was low forest age.

基于大兴安岭北部林区19块样地内104株天然兴安落叶松实测生物量数据，建立兴安落叶松天然林地上总量和分量相容性生物量模型，分别采用权函数和联立线性方程组消除方程的异方差和度量误差。结果表明：1）含度量误差的单木生物量相容性模型能解决总量生物量模型和分量生物量模型不兼容的问题，而且模型的预估精度高于经验模型；2）所建模型参数的决定系数 R 2 和模型偏差统计量，估计值的标准差SEE、平均估计误差MPE、平均相对偏差ME、平均相对偏差绝对值MAE分别为0.907~0.947，1.887~17.368，1.011%~2.703%，-4.937%~6.998%，5.408%~10.886%；3）对大兴安岭北部兴安落叶松天然林样木实测值进行统计分析，得到兴安落叶松天然林单木干材生物量占地上生物量的60.37%~76.80%，所占比例随年龄增加先增加再减小。树皮生物量占地上生物量的7.15%~20.11%，所占比例随年龄增加而减小；树枝生物量占地上生物量的8.51%~14.29%，所占比例随年龄增加基本呈现增加趋势；树叶生物量占地上生物量的5.12%~7.09%，在低林龄期时所占比例最大。

... 通过分级控制建立单木总生物量模型,能够有效消除度量误差,解决生物量总量模型和各器官生物量模型不兼容的问题^[23] ...

... 在无竞争存在时,会增加地上各器官生物量分配^[17],树干在立木组分中占有较大比重^[23],但树干生物量分配比例在不同龄组间差异却非常显著^[7] ...

2013

0.0

曾鸣, 聂祥永, 曾伟生. 中国杉木相容性立木材积和地上生物量方程[J]. 林业科学, 2013, 49(10): 74-79.

[ZENG

, NIE X

, ZENG W

. Compatible tree volume and aboveground biomass equations of Chinese fir in China. Scientia Silvae Sinicae, 2013, 49(10): 74-79. ]

... 此外,还有学者采用混合模型和误差变量联立方程组方法^[24,25,26],构建了不同区域、不同起源立木生物量的通用性方程 ...

2015

0.0

符利勇, 唐守正, 张会儒, 等. 东北地区两个主要树种地上生物量通用方程构建[J]. 生态学报, 2015, 35(1): 150-157.

[FU L

, TANG S

, ZHANG H

, et al. Generalized above-ground biomass equations for two main species in Northeast China. Acta Ecologica Sinica, 2015, 35(1): 150-157. ]

Individual tree biomass equations have been frequently used in ecological and forestry research over the last 60 years. They represent a powerful tool to understand forest productivity, nutrient cycling, and carbon sequestration, and they are used to estimate other structural and functional characteristics of forest ecosystems. Current attempts to develop above-ground biomass equations for Larix forests in northeast China have been mainly focused on only one species or applied to the genus Larix as a whole. However, generalized above-ground biomass equations for Larix could be used to estimate the average relationship between above-ground biomass and different independent variables and also variations among different Larix species. We developed generalized biomass equations for different Larix species by using Larix olgensis and Larix gmelinii . In this study, a total of nine tree variables that were able to predict above-ground biomass in Larix species were examined using biomass equations. The results show that D, H , and CW contributed significantly to predict above-ground biomass. Therefore, three combinations of these variables, including D alone; D and H ; and D, H, and CW , were selected as independent variables to develop univariate, bivariate, and trivariate biomass generalized equations, respectively. The trivariate biomass generalized equations predicted above-ground biomass better than the other two equation types, while the predictive power of the univariate equation was the worse than the rest. Theoretically, the prediction accuracy of trivariate biomass equations could be further increased by adding stands or tree variables; however, including an excessive number of parameters in the biomass equations may hinder computation convergence and reduce the speed required to estimate model parameters. Furthermore, including many stands or tree variables would increase the cost and time required to conduct forest inventories. Therefore, determining the appropriate number of independent variables able to provide the level of accuracy required by forest managers is essential in forest modeling. A parsimonious model with reliable accuracy of prediction has been suggested as a reasonable approach for efficient forest management. For this reason, D, H, and CW were finally selected as independent variables for the generalized biomass equations developed in this study. In general, the biomass of individual trees with the same D would depend on the region studied and the origin of the tree. Thus, the generalized above-ground biomass equations developed for different Larix species in northeast China consider this inter-regional variation by using a dummy variable. To reduce heteroskedasticity in the data, we used weighted least square regressions. The results showed that the predictive precision of the biomass equations could be improved by adding predictor variables. Regardless of the traditional biomass equation used, both generalized equations considering only tree species and those considering tree species, tree origin, and region showed the highest prediction power. In addition, the accuracy for predicting above-ground biomass did not differ among univariate, bivariate, and trivariate equations when tree species, tree origin, and region were considered. On the basis of these results, the trivariate generalized biomass equation that considers tree species, tree origin, and region was believed to be the best option for estimating the biomass of L. olgensis and L. gmelinii .

目前,东北落叶松地上生物量方程主要采用分树种或把不同树种归为一体的方法,但是,既能反映落叶松生物量与自变量的平均关系,又能反映不同树种间生物量差异程度的通用性落叶松生物量方程迄今尚未构建。因此,以东北地区兴安落叶松和长白落叶松地上生物量数据为研究对象,构建一元(自变量为胸径)、二元(自变量为胸径和树高)和三元(自变量为胸径、树高和冠幅)的不同树种生物量通用方程。由于起源和地域的不同,生物量可能会存在一定程度差异,进而,在所构建的不同树种生物量通用方程的基础上,考虑起源和地域的差异,利用哑变量方法构建既能考虑不同树种又能考虑林分起源和不同地域的东北落叶松地上生物量通用方程,并利用加权最小二乘法剔除方程异方差。结果表明:通过哑变量方法构建不同树种生物量模型方法可行;不论是传统的生物量方程,还是只考虑树种或同时考虑树种、起源和地域的通用生物量方程,增加自变量能提高方程预测效果,即,三元生物量方程预测精度最高,二元生物量方程次之,一元生物量方程最低;当同时考虑树种、起源和地域时,方程预测精度最高,只考虑树种的生物量通用方程次之,传统生物量方程最低。因此,如果数据允许,建议构建考虑不同树种、起源和地域的三元生物量方程估计东北地区长白落叶松和兴安落叶松地上生物量。

... 此外,还有学者采用混合模型和误差变量联立方程组方法^[24,25,26],构建了不同区域、不同起源立木生物量的通用性方程 ...

... 符利勇等^[25]通过哑变量方法基于不同数量的自变量构建了相容性生物量模型,曾伟生等^[26]利用线性混合效应模型实现了不同起源树种生物量模型通用性,而非线性混合效应模型联立方程组法则缺乏相应的算法^[25] ...

2011

0.0

曾伟生, 唐守正, 夏忠胜, 等. 利用线性混合模型和哑变量模型方法建立贵州省通用性生物量方程[J]. 林业科学研究, 2011, 24(3): 285-291.

[ZENG W

, TANG S

, XIA Z

, et al. Using linear mixed model and dummy variable model approaches to construct generalized single-tree biomass equations in Guizhou. Forest Research, 2011, 24(3): 285-291. ]

Based on the above-ground biomass data of Chinese fir ( Cunninghamia lanceolata ) and Masson Pine ( Pinus massoniana ) plantations in Guizhou Province, the generalized single-tree biomass equations suitable for different species and regions (central region and other region) were established using linear mixed model and dummy variable model methods, which provided effective approaches to simplify the biomass modeling. The results show that the above-ground biomass estimates of individual trees with the same diameter are different in some extent among different tree species and geographic regions, and linear mixed model with random parameters and dummy model with specific (local) parameters are better than population average model; and linear mixed model and dummy variable model approaches are almost same effective and may be applied to develop other generalized models such as tree volume equations.

以贵州省人工杉木和马尾松地上生物量数据为例,通过利用线性混合模型和哑变量模型方法,建立了适合不同树种和区域(中心区和一般区)的通用性立木生物量方程,为简化生物量建模工作提供了有效途径。结果表明,相同直径林木的地上生物量估计值随树种、区域的不同存在一定程度的差异,带随机参数的线性混合模型和带特定参数的哑变量模型比总体平均模型的精度高;线性混合模型和哑变量模型方法均同等有效,可推广应用于其它通用性模型(如材积方程)的建立。

... 此外,还有学者采用混合模型和误差变量联立方程组方法^[24,25,26],构建了不同区域、不同起源立木生物量的通用性方程 ...

2017

0.0

王冬至, 张冬燕, 张志东, 等. 塞罕坝华北落叶松人工林断面积预测模型[J]. 北京林业大学学报, 2017, 39(7): 30-36.

[WANG D

, ZHANG D

, ZHANG Z

, et al. Prediction model for basal area of Larix principis-rupprechtii plantation in Saihanba of Hebei Province, northern China. Journal of Beijing Forestry University, 2016, 52(1): 30-36. ]

摘　要：如何实现林分水平和单木水平预测林分断面积的兼容性,并提高不同水平断面积模型的预估精度,在森林经营过程中是一个亟待解决的科学问题。本文以华北暖温带华北落叶松人工林为研究对象,运用105块连续观测的固定样地数据,首先采用Gauss-Newton算法建立林分水平和单木水平断面积生长模型;其次分别采用不同形式的逻辑斯蒂方程对单木生存概率方程进行拟合;最后将不同水平最优预测模型进行组合并建立组合方程,采用最小二乘法估计组合方程参数,以提高对不同水平断面积的预测精度。结果表明：在约束参数法中,林分密度模型、林分断面积预测模型和单木断面积模型均具有较好的预测效果,并均能解释90%以上的变异;在分解法中采用逻辑斯蒂方程来预测单木生存概率和林分密度,经检验获得的ROC曲线下面积为0.906,表明该方程可以较好地预测林木生存概率;在组合预测法中,采用不同水平的最优模型进行组合后的预测效果最佳。在预测林分密度和断面积时,组合预测方程预测精度最高,林分水平模型预测精度次之,单木水平模型预测精度最低。组合预测法能够预测不同水平下的林分密度、立木生存概率、林分断面积及单木断面积,提高了模型预测精度,为预测林分生长动态、空间结构变化及经营效果评价等提供参考依据。

... 2 mm^[27] ...

2017

0.0

2007

0.0

2011

0.0

2006

0.0

... Wang等^[31]研究表明选择哑变量方法和混合模型方法均可实现模型通用性且预测结果相同 ...

2015

0.0

董利虎, 李凤日, 宋玉文. 东北林区4 个天然针叶树种单木生物量模型误差结构及可加性模型[J]. 应用生态学报, 2015, 26(3): 704-714.

[DONG L

, LI F

, SONG Y

. Error structure and additivity of individual tree biomass model for four natural conifer species in Northeast China. Chinese Journal of Applied Ecology, 2015, 26(3): 704-714. ]

2011

0.0

巨文珍, 王新杰, 孙玉军. 长白落叶松林龄序列上的生物量及碳储量分配规律[J]. 生态学报, 2011, 31(4): 1139-1148.

[JU W

, WANG X

, SUN Y

. Age structure effects on stand biomass and carbon storage distribution of Larix olgensis plantation. Acta Ecologica Sinica, 2011, 31(4): 1139-1148. ]

It is essential to study forest biomass, which is an important quantity character for forest ecosystems. Although intense studies have been carried out on the biomass of Larix olgensis plantations, little attention was paid on the dynamics of biomass and carbon storage with age structure variation. We researched the age structure effect on forest biomass and carbon storage by investigating its vertical distribution of Larix ologensis plantations. For many years excessive cutting and slighting fostering, the stand quality and the function of forest ecosystem have descended in Dong Zhelenghe forestry centre of Yi Chun, China. By analyzing the vertical distribution biomass of different components for Larix ologensis plantations in a homogenous site condition, the biomass distribution in age sequence was studies. The study was aimed to provide the quantitative reference for improving the productivity and carbon storage by adjusting the stand structure. The proportions of trunk, bark and living branch biomass were less correlated with age structure, but that of leaves decreased with stand growth significantly. We analyzed vertical distribution of biomass for different components in varying-age stands. The relationship between biomass and tree height showed a uniform pattern among age structures. The bark- and trunk-biomass descended with tree height, and that of living branches and leaves concentrated in middle of tree canopy, while the dead-branches biomass appeared less difference vertically. The biomass proportions of coarse, medium and fine roots decreased with stand age, but opposite for main-root biomass. The relationship between stand biomass and stock volume was fitted as W =0.4909 M +9.6624( R 2 =0.8893). We know from the estimated results that the total biomass of Larix olgensis young plantations in the study area was 1273.72t/hm 2 , and carbon storage 656.98 t/hm 2 .The total biomass of middle-age forests was 15480.13 t/hm 2 , or carbon storage 7984.65 t/hm 2 as. Total biomass of the pre-mature and mature plantations was 7684.41t/hm 2 , or carbon storage was 3963.62t/hm 2 as. The forest biomass or carbon storage is expected to increase under shifting age structures and new management strategies.

由于多年来的过量采伐和重采轻育,伊春东折棱河林场人工长白落叶松林分质量普遍下降,森林生态功能严重衰退。结合对该研究地同一立地类型的人工长白落叶松林( Larix ologensis )林木各组分生物量垂直分配规律的分析,研究了其生物量在年龄序列上的分布及分配规律,为提高其林分生物量及碳储量采取相应的抚育管理措施提供一定的理论基础。结果表明,处于中龄、近熟及成熟林中的林木树干、树皮及活枝生物量所占比例受年龄影响较小,而叶生物量随林龄增大呈现明显递减变化;不同年龄长白落叶松的垂直分布规律基本一致:其树皮及树干生物量随树高增大呈现递减规律,其活枝及叶生物量主要集中分布于树冠中部,而其死枝生物量未呈现明显分布规律;长白落叶松根系生物量随着林分年龄的增大,其粗根、中根及细根所占比例呈现递减规律,而其大根所占比例随年龄的增大基本呈增大趋势。通过统计分析得出,长白落叶松生物量与林分蓄积的最优模型为: W =0.4909 M +9.6624( R 2 =0.8893),进而估算得出:研究区域幼龄长白落叶松林分生物量为1273.72 t/hm 2 ,碳储量为656.98 t/hm 2 ;中龄长白落叶松林分生物量为15480.13 t/hm 2 ,碳储量为7984.65 t/hm 2 ;近熟、成熟龄长白落叶松林分生物量为7684.41 t/hm 2 ,碳储量为3963.62 t/hm 2 。随林分结构的改善以及中龄、近熟及成熟林分的不断增加,生物量及碳储量会相应增加。

... 2 各器官生物量分配树木各器官生物量直接反映光合产物积累量,并影响最优化分配格局^[33] ...

... 07,与部分学者^{[7,13,14,17,33]}研究结果相似 ...

... 树木各器官生物量分配比例是动态变化的^[33],通常会受到诸多生物学和非生物学因素限制,如光照、水分、养分、年龄、密度及立木大小等^[4,34] ...

2008

0.0

黄从德, 张健, 杨万勤, 等. 四川省及重庆地区森林植被碳储量动态[J]. 生态学报, 2008, 28(3): 966-975.

[HUANG C

, ZHANG

, YANG W

, et al. Dynamics on forest carbon stock in Sichuan Province and Chongqing City. Acta Ecologica Sinica, 2008, 28(3): 966-975. ]

Forest in Sichuan (including Chongqing) locate in the eastern of Tibet Plateau honored by the third pole in the world. As a principal part of SW forest region, the second largest forest region in China, the forest carbon stock plays an important role in global carbon cycle, implying that it is important for forest carbon stock evaluation to understand the role of the forest in mitigating climate change. Therefore, carbon stocks in Sichuan (including Chongqing) forest at different phases were evaluated to understand the contribution of Sichuan forest to mitigate climate change, employing the methods of establishing the model of forest biomass and volume, measuring carbon content in different stands and integrating four provincial forest inventory data in Sichuan (including Chongqing). Mean carbon content of the studied forest stands was 51.09%, ranging from 46.75% to 54.89% ,and depending on the forest stands. On average, carbon content was 52.82% in the coniferous forest, which was significantly higher than that in the broadleaved forest (49.37%). Forest carbon stock in Sichuan increased 140.53 Tg C from 383.04 TgC in 1998 to 523.57 TgC in 2003 and by 2.11% annually during the study period, which was more 0.22% than that of the mean increment in China, implying that Sichuan (including Chongqing) forest is carbon sink in atmospheric carbon dioxide, and contributes to climate change mitigation. Correspondingly, average carbon density in the forest was 38.93, 38.68, 39.17 MgC/hm2, and 41.66 MgC/hm2, respectively, and showed the increasing trend during the period of four forestry inventories, implying that the potential of carbon sink in Sichuan (including Chongqing) forest was increasing. Carbon stock in mature forest showed the declining trend in the study period, which accounted for 64.15%, 63.89%, 65.33%, and 60.82% of the total in the corresponding phase, respectively, while that in young and middle-aged forest showed the opposite, showing that the study forest has a strong potential of carbon sequestration. Meanwhile, the potential of carbon sequestration in the plantation increased continuously although natural forest stored carbon more than 90% for the same stage, resulting that annual increment of carbon stock in the plantation was 7.17% in comparison with 1.83% in natural forest. The results showed that man-made forest played an important role in enhancing forest carbon sequestration in the study region. Furthermore, the results also showed that Sichuan the study forest played an important and irreplaceable role in enhancing national forest carbon sequestration due to higher carbon sequestration in the forest in comparison with national level.

四川省及重庆市地区森林植被是我国第二大林区-西南林区的主体，位于“世界第三极”——青藏高原东缘。在建立森林乔木层生物量与蓄积量回归模型的基础上，按林分类型测定含碳量，结合四川4次森林资源清查数据，估算了不同时段的碳储量。各林分类型含碳量在46.75%～54.89%之间，平均含碳量为51.09%，针叶林平均含碳量（52.82%）大于阔叶林（4937%）；四川森林植被碳储量从1988年的383.04TgC增加到2003年的523.57TgC，增加了140.53TgC，年均增长率2.11%，比全国年均增长率高出0.22%，表明四川森林植被是CO2的一个汇。4次调查的森林植被平均碳密度分别为38.93、3868、3917、41.66MgC/hm2，呈现增加趋势，表明森林植被的碳汇功能不断加强；成熟林碳储量占同期的64.15%、63.89%、65.33%、60.82%，但所占比重呈下降的趋势，幼中林碳储量的比重不断上升，表明森林植被的碳吸存潜力大；森林植被碳储量主要分布在天然林中，占同期碳储量的90%以上，但人工林的碳储能力正在逐步提高，人工林碳年均增长率（7.17%）明显大于天然林（1.83%），表明人工林将在研究区域森林植被碳汇功能中扮演重要的角色。研究区森林植被碳储量占同期全国碳储量的比例呈增加趋势，可见，研究区森林植被在全国森林碳汇中具有重要的作用和地位。

... 树木各器官生物量分配比例是动态变化的^[33],通常会受到诸多生物学和非生物学因素限制,如光照、水分、养分、年龄、密度及立木大小等^[4,34] ...

2012

0.0

... 在生长过程中,林木会不断调节各器官生物量比例以最大化获得受限资源^[35,36] ...

2007

0.0

王平, 王天慧, 周道玮, 等. 植物地上竞争与地下竞争研究进展[J]. 生态学报, 2007, 27(8): 3489-3499.

[WANG

, WANG T

, ZHOU D

, et al. A literature review on the above-and below-ground competition. Acta Ecologica Sinica, 2007, 27(8): 3489-3499. ]

Plants competes for both above-ground and below-ground resources. However, there are so many conflicting reports regarding the mechanisms of competition in both natural plant population and agricultural plant communities. In this paper, we reviewed some existing literatures dealing with above-and below-ground competitions, including their experimental methodologies as well as the various indices employed in the interpretation of the intensity of both above-and below-ground competitions. It is hoped that this review will serves as a further reference point in which researchers can consider the potential directions for future research in competition studies. Optimal allocation models and theories for both under above-and below-ground competitions, and the variations as well as the trade-off between above- and below-ground competitions, including the effect of heterogeneous resources on these two different spatially competitive environments were compared. Furthermore some of the experimental methodologies in the study of competition such as the divided pot technique, row technique and target technique were reviewed with particular emphasis being placed on their advantages and limitations. In conclusion we suggested that, the following factors viz. the physiological characteristics and developmental status of experimental plants, environmental productivity range and length of competition persistence, should be considered in future studies of competition. Researches on the below-ground competition, process of root interaction and influence are now booming.

植物地上光竞争和地下水分与营养的竞争过程十分复杂，并且与竞争机制密切相关。从地上和地下竞争理论、两种竞争过程的相互作用机制以及分离地上和地下竞争的研究方法和表达指标等几个方面综述和分析目前的研究状况，以期为国内研究者在本领域进一步展开实验提供理论依据和实验设计参考。总结了与地上、地下相对竞争强度有关的优化分配理论，地上、地下竞争随生产力梯度的变化，资源异质性对地上、地下竞争机制的影响。介绍了地上竞争和地下竞争相互作用类型以及目前提出的两种作用机制。对常用的3种分离地上、地下竞争的方法：盆分隔、间植分隔和目标植分隔法以及表达竞争强度和竞争重要性的指标和公式进行了归纳。提出未来的研究内容，认为在开展此类研究时，应考虑到实验植物的生理学特性、发育状况、立地生产力跨度范围以及竞争持续时间等方面因素，并认为发展地下竞争研究、深入探讨根系间相互作用的影响因子和过程是当前的研究热点。

... 在生长过程中,林木会不断调节各器官生物量比例以最大化获得受限资源^[35,36] ...

2012

0.0

黎磊, 周道玮, 盛连喜. 植物种群自疏过程中构件生物量与密度的关系[J]. 生态学报, 2012, 32(13): 3987-3997.

[LI

, ZHOU D

, SHENG L

. Allometric relationship between mean component biomass and density during the course of self-thinning for fagopyrum esculentum populations. Acta Ecologica Sinica, 2012, 32(13): 3987-3997. ]

Body size ( M ) was specifically referred to above-ground biomass of individual plant for both power law of self-thinning and energy equivalence law for plant populations in most studies. Little is known about the biomass-density relationships with respect to below-ground part and other plant components, such as stem, leaf and reproductive part during the course of self-thinning, although they were very important. The self-thinning law can also be defined as component biomass, below-ground biomass and total biomass when all biomasses of all yield components are measured, such as leaf, stem, reproductive biomass and below-ground biomass. Subsequently, the competition effects of total biomass or each plant component can be observed during the course of self-thinning as required. Since growth in plants is a modular process, it is rational ecologically to examine biomass-density relationships not only at population and individual levels, but also at plant part level. The growth patterns of plant components, such as stems, leaves and reproductive parts, as well as roots, in relationship with plant density were studied with Fagopyrum esculentum populations in a pot experiment. There were 3 plant densities (8000, 24000 and 48000 plants/m 2 ) with 4 replicates in a randomized complete design. There were 6 harvesting times with 4 pots being destructively harvested at each harvesting time. Results showed that the values of self-thinning exponents were -1.293 and -1.253 for mean above-ground biomass and total biomass, respectively, during the course of population development. These values, which were not significantly different from -4/3, can be regarded as evidence in favor of the -4/3 power law of self-thinning. The allometric exponents were -1.128, -1.263, -1.524 and -2.005 for mean biomass of roots, stems, leaves and reproductive parts, respectively. There were no significant difference between γ roo t and -1( P > 0.05), γ stem and -4/3( P > 0.05), γ leaf and -3/2( P > 0.05),but γ reproductive was significantly different from -3/2, -4/3 or -1. It is suggested that there is no universal biomass-density relationship associated with plant components. Competition within the population affects plant development and alters the biomass allocation patterns of plants and may lead to different biomass-density relationships for plant components in the population. Specific allometric relationships between plant component biomass and above-ground biomass can also resulted in slopes of the self-thinning lines which are different from -3/2 or -4/3. Populations of Fagopyrum esculentum obeys the law of energy equivalence during the course of self-thinning for above-ground biomass or total biomass, but for below-ground biomass.

不论是在对植物种群自疏规律还是在对能量守衡法则的研究中,个体大小( M )大多针对植物地上部分生物量,地下部分和构件生物量及其动态十分重要又多被忽视。以1年生植物荞麦为材料研究了自疏种群地下部分生物量、包括地下部分的个体总生物量以及各构件生物量与密度的关系。结果表明:平均地上生物量和个体总生物量与密度的异速关系指数( γ above-ground 和 γ individual )分别为-1.293和-1.253,与-4/3无显著性差异( P > 0.05),为-4/3自疏法则提供了有力证据;平均根生物量-密度异速指数 γ root (-1.128)与-1无显著性差异( P > 0.05),与最终产量恒定法则一致;平均茎生物量-密度异速指数 γ stem (-1.263)接近-4/3( P > 0.05),平均叶生物量-密度异速指数 γ leaf (-1.524)接近-3/2( P > 0.05),分别符合-4/3自疏法则与-3/2自疏法则;而繁殖生物量与密度的异速关系指数 γ reproductive (-2.005)显著小于-3/2、-4/3或-1( P < 0.001)。因此,不存在一个对植物不同构件普适的生物量-密度之间的关系。光合产物在地上和地下构件的生物量分配格局以及构件生物量与地上生物量之间特异的异速生长关系导致不同构件具有不同的自疏指数。无论对于地上生物量还是个体总生物量,荞麦种群能量均守衡,而对于地下生物量,荞麦种群能量不守衡。

... 立木对光照、水分和养分竞争能力的高低是通过各器官生物量分配实现的^[37],其中枝、叶、根生物量分配光照、水分和养分条件有显著相关性^[38],当光照成为主要限制因子时,立木将更多生物量分配给枝和叶,以尽可能多的获取光照 ...

2002

0.0

2005

0.0

... 当水分或养分成为最主要的限制因子时,更多生物量分配给根,以获取更多土壤水分或养分^[39,40,41] ...

2015

0.0

仇瑶, 常顺利, 张毓涛, 等. 天山林区六种灌木生物量的建模及其器官分配的适应性[J]. 生态学报, 2015, 35(23): 7842-7851.

[QIU

, CHANG S

, ZHANG Y

, et al. Biomass estimation modeling and adaptability analysis of organ allocation in six common shrub species in Tianshan Mountains forests, China. Acta Ecologica Sinica, 2015, 35(23): 7842-7851. ]

Estimation modeling of the total biomass of shrubs is associated with certain difficulties. Moreover, merely studying the effect of organ allocation adaptability on shrub biomass is not sufficient. Thus, to investigate the effectiveness of biomass estimation modeling on organ allocation in plants, we focused on six common shrub species found in the forests of Tianshan Mountains, northwest China. To conduct a community investigation, we selected three sample areas in the eastern, central, and western regions of Tianshan Mountains. A number of whole standard plants from six shrub species were harvested to determine total biomass, which was divided into the, biomass of the roots, branches, and leaves, along with different classes of root diameter. D 2 H (the square of the diameter multiplied by height) and V (the area of the crown multiplied by height) were selected as the independent variables in the estimation models. Optimal estimation models for the total biomass of the six shrub species were constructed using regression analysis. These models were used to compare differences in total biomass allocation to vegetative organs and in biomass allocation to roots of each root diameter class in the shrub species. The following results were obtained. First, the total biomass of Berberis heteropoda , Lonicera hispida , and Cotoneaster melanocarpus was approximately 8.48 to 9.01 kg, whereas that of Rosa spinosissima , Spiraea hypericifolia , and Juniperus pseudosabina was approximately 2.71 to 3.20 kg. Second, the optimal estimation models for the total biomass of R. spinosissima , S. hypericifolia , and C. melanocarpus were functions based on V as an independent variable, whereas those for B. heteropoda , L. hispida , and J. pseudosabina were functions based on D 2 H as an independent variable. The value of R 2 for each estimation model was greater than 0.850, and all the models reached a high degree of accuracy at the 0.05 significance level. Third, differences in the proportional allocation of total biomass to roots and branches of the six shrub species were not significant, whereas that to leaves was significant at the 0.05 significance level. The root biomass of all six shrub species decreased with decreasing root diameter class, with significant differences in the proportional allocation of biomass to roots in roots with a diameter greater than 2 mm (significant at the 0.05 and 0.01 significance levels for roots with diameters greater than 20 mm). For all examined shrub species, we conclude that the differences in total biomass allocation to vegetative organs and in biomass allocation to the roots of each diameter class reflect adaptive strategies to their respective habitats.

灌木全株生物量估算模型的构建仍存在一定困难,对灌木生物量在器官分配上所体现的适应性研究也不够充分。以天山林区6种常见灌木为研究对象,在天山的东段、中段、西段林区分别设置样地进行群落调查,由此以全株收获法取得6种常见灌木若干标准株的全株、根、枝、叶及各径级根的生物量,将 D 2 H (地径平方与高度的乘积)与 V (冠幅面积与高度的乘积)分别选为估测模型的自变量,通过回归分析法建立了各种灌木全株生物量的最优估算模型,然后比较了此6种灌木全株生物量在营养器官上分配差异以及根系生物量在径级上的分配差异。结果表明:(1)天山林区6种常见灌木中,小檗( Berberis heteropoda Schrenk)、忍冬( Lonicera hispida Pall. ex Roem. et Schuet.)、栒子( Cotoneaster melanocarpus Lodd.)的全株生物量约为8.48-9.01 kg,蔷薇( Rosa spinosissima L.)、绣线菊( Spiraea hypericifolia L.)、方枝柏( Juniperus pseudosabina Fisch. et Mey.)的全株生物量约为2.71-3.20 kg;(2)蔷薇、绣线菊、栒子的全株生物量最优估测模型是以 V 为自变量的函数,小檗、忍冬、方枝柏的全株生物量最优估测模型是以 D 2 H 为自变量的函数,各模型 R 2 值均在0.850以上,且在 P P P P < 0.01水平);(4)6种灌木全株生物量在营养器官上的分配差异以及根系生物量在径级上的分配差异均体现了各物种对其生境选择的适应策略。

... 当水分或养分成为最主要的限制因子时,更多生物量分配给根,以获取更多土壤水分或养分^[39,40,41] ...

2017

0.0

朱桂丽, 李杰, 魏学红, 等. 青藏高寒草地植被生产力与生物多样性的经度格局[J]. 自然资源学报, 2017, 32(2): 210-222.

[ZHU G

, LI

, WEI X

, et al. Longitudinal patterns of productivity and plant diversity in Tibetan alpine grassland s. Journal of Natural Resources, 2017, 32(2): 210-222. ]

... 当水分或养分成为最主要的限制因子时,更多生物量分配给根,以获取更多土壤水分或养分^[39,40,41] ...

2008

0.0

安慧, 上官周平. 密度对刺槐幼苗生物量及异速生长模式的影响[J]. 林业科学, 2008, 44(3): 151-155.

[AN

, SHANGGUAN Z

. Effects of density on biomass and allometric pattern of Robinia pseudoacacia seedling. Scientia Silvae Sinicae, 2008, 44(3): 151-155. ]

The aboveground and underground biomass and allometry relationship between plant height and stem diameter of Robinia pseudoacacia seedling under different planting density were studied. Experiments were designed for cultivated R. pseudoacacia seedling under different planting density (including row spacing 30 cm, and planting distance 15, 20, 25, 30 cm) in March 2005. The seedlings were watered and fertilized regularly to maintain growth under limited resources. At the beginning of September 2005, the seedling leaves, stems and roots were harvested and weighed separately to obtain the wet and dry biomass. The result showed that the biomass of roots, stems and leaves of R. pseudoacacia increased with planting distance increase under row spacing 30 cm. Ratio of root to shoot of R. pseudoacacia increased with planting distance increase, and was all less than 1 under different planting distance. Ratio of root to shoot of R. pseudoacacia was significant between planting distance 15 cm and other distances, but not significant among planting distance 20, 25 and 30 cm. The less effects of low density on aboveground biomass, underground biomass and resource utilization of R. pseudoacacia. The plant height and stem diameter of R. pseudoacacia seedling increased with planting distance increase ( p y = a + bx . However, under high density, there is strong intraspecific competition between individual plants, the relationship between height and diameter is nonlinear allometry and its allometric function can be expressed as y = ax 2 + bx + c .

刺槐(Robinia pseudoacacia)具有较强的生态适应性和抗逆能力,是黄土高原植被恢复和生态重建的主要优良树种之一(程积民等,2002;陈云明等,2002).

... 立木大小和密度导致树木间产生空间和资源竞争,从而影响树木的可塑性,进而导致各器官的生物量分配比例变化^[42,43] ...

2008

0.0

黄迎新, 赵学勇, 张洪轩, 等. 沙米表型可塑性对土壤养分、水分和种群密度变化的响应[J]. 应用生态学报, 2008, 19(12): 2593-2598.

[HUANG Y

, ZHAO X

, ZHANG H

, et al. Responses of agriophyllum squarrosum phenotypic plasticity to the changes of soil nutrient and moisture content sand population density. Chinese Journal of Applied Ecology, 2008, 19(12): 2593-2598. ]

... 立木大小和密度导致树木间产生空间和资源竞争,从而影响树木的可塑性,进而导致各器官的生物量分配比例变化^[42,43] ...