新疆塔里木河流域洪水发生率非平稳性特征及气候变化影响研究

引用本文

顾西辉, 张强, 孔冬冬, 刘剑宇. 新疆塔里木河流域洪水发生率非平稳性特征及气候变化影响研究[J].自然资源学报, 2016,31(9): 1499-1513
GU Xi-hui, ZHANG Qiang, KONG Dong-dong, LIU Jian-yu. Nonstationarity of Flooding Processes in the Tarim River Basin and Climate-related Impacts[J]. Journal of Natural Resources, 2016,31(9): 1499-1513 复制到剪切板

DOI:10.11849/zrzyxb.20151164

Permissions

《自然资源学报》编辑部所有

新疆塔里木河流域洪水发生率非平稳性特征及气候变化影响研究

顾西辉¹, 张强^2,^*, 孔冬冬¹, 刘剑宇¹

1. 中山大学水资源与环境系,广州 510275

2. 北京师范大学 a. 环境演变与自然灾害教育部重点实验室,b. 地表过程与资源生态国家重点实验室,c. 减灾与应急管理研究院,北京100875

第一作者简介：顾西辉（1990- ）,男,河南信阳人,博士研究生,中国自然资源学会会员（S300001710M）,主要从事区域水循环与水资源演变研究。E-mail: guxihui421@163.com

*通信作者简介：张强（1974- ）,男,山东沂水人,博士,教授,博士生导师,主要从事流域气象水文学研究、旱涝灾害机理、流域地表水文过程及其对气候变化的响应机制与机理以及流域生态需水等领域的研究工作。E-mail: zhangq68@mail.sysu.edu.cn

收稿日期:2015-10-23 网络出版日期:2016-09-20

基金:国家杰出青年科学基金项目（51425903）; 广东省城市化与地理环境空间模拟重点实验室开放基金; National Natural Science Foundation of China, No.51425903; Open Fund of Guangdong Provincial Key Laboratory of Urbanization and Geo-simulation

摘要

新疆洪水灾害近年来有加剧趋势,但其特征与机理尚未有深入探讨。论文利用核估计和Bootstrap方法深入分析新疆塔里木河（塔河）流域洪水发生率的非平稳性及不确定性,同时采用广义可加模型（GAMLSS）构建洪水发生频率与协变量（大气环流因子、降水和气温指标等）的关系并定量辨识主要影响因子。研究表明：1）塔河流域洪水在1960年代左右和1990年代左右两个时期高频发生,两个洪水高发期之间洪水发生次数多为2或3次,且与极端降水发生次数较为吻合;2）洪水发生率呈现显著非平稳性,从1990年左右洪水发生次数持续上升,并达到峰值,表明洪水发生频率及强度呈加剧趋势;3）冬季AMO和AO是影响新疆塔河流域洪水发生的重要因子,而冬季NAO和SOI则是影响塔河流域5个州的洪水发生次数最为显著的大气环流指标。论文研究可为新疆塔河流域洪灾预测与预警及流域洪水管理提供关键理论依据。

关键词: 核估计; GAMLSS; 洪水发生率; 非平稳性; 塔里木河流域

中图分类号:P333.2;P467 文献标志码:A 文章编号:1000-3037(2016)09-1499-15

Nonstationarity of Flooding Processes in the Tarim River Basin and Climate-related Impacts

GU Xi-hui¹, ZHANG Qiang², KONG Dong-dong¹, LIU Jian-yu¹

1. Department of Water Resources and Environment, Sun Yat-sen University, Guangzhou 51275, China

2. a. Key Laboratory of Environmental Change and Natural Disaster, b. State Key Laboratory of Earth Surface Processes and Resource Ecology, c. Academy of Disaster Reduction and Emergency Management, Beijing Normal University, Beijing 100875, China

Abstract

Aggravation of flood has been observed in Xinjiang, China. However, no reports are available addressing changing properties and related mechanisms. In this paper, flooding frequency in the Tarim River Basin, the largest inland arid river basin in China, was analyzed by using the Kernel smoothing technique and bootstrap resampling method. Besides, the flood frequency and extreme precipitation events were analyzed by using the POT method. Both stationary and non-stationary models were conducted by using GAMLSS (Generalized Addi-tive Models for Location, Scale and Shape) to model the flood frequency and its relations with explanatory variables (e.g. time, climate index, precipitation and temperature). The results indicated that: 1) The flood occurrence in the Tarim River Basin clustered in two periods, i.e. ~1960s and ~1990s with around 2-3 fluctuations. 2) The change of flood frequency is nonstationary process. Persistent increase of flood frequency can be observed since 1990s and the flood frequency gradually reached its peak value, implying evident aggravation of floods in terms of magnitude and frequency. 3) Winter AMO and AO are the principle influencing factors of the change of flood frequency, while winter NAO and SOI are two critical climate indices influencing flood frequency in the Tarim River Basin. The results of this study can provide great scientific and theoretical support for the management of floods and mitigation of flood hazards.

Keyword: Kernel estimation; GAMLSS; flood frequency; non-stationarity; Tarim River Basin

Show Figures

全球变暖及其对生态、水资源、人类社会等的影响已引起人们的广泛关注^[1], 尤其是在气候暖化影响下, 极端水文气象事件（例如洪水和干旱）发生频率与强度有加剧化趋势^[2]。已有较多研究开展有关洪水过程的研究, 尤其是洪水过程的非平稳性研究方面, 已成为极值过程研究的热点。Milly等^{[3, 4, 5]}研究认为, 在洪水管理中, 洪水过程的平稳性假设受到越来越多的挑战, 需要在洪水过程研究中考虑非平稳性问题。顾西辉等考虑了洪峰序列中的趋势性在洪水风险分析中的影响^[6]; 冯平等^[7]用Copula函数构建洪峰和洪量的非一致性频率分析模型。由以上研究可以看出, 以往的研究多关注洪峰量级的非平稳性, 而对洪水发生频率的非平稳性研究较少, 而洪水频率的研究对于防洪及洪灾管理具有重要意义。

新疆位于西北内陆干旱区, 近几十年来, 受全球气候变化影响, 新疆气候特征发生了显著变异。施雅风等认为西北地区气候可能由暖干转向暖湿^[8]。冯思等进一步指出气温上升导致水循环加速, 进而引起新疆地区降水量增加^[9]。慈晖等采用多个极端降水指标分析了新疆极端降水过程, 发现强降水过程变幅增大, 易导致洪旱灾害等极端气象水文事件发生^[10]。新疆降水过程的变化导致洪涝灾害在近几十年呈显著上升趋势^[11]。有研究表明：新疆洪水发生频次增加, 洪峰流量增大^[12], 并且洪灾导致的受灾面积也呈显著增加趋势^{[13, 14]}。塔里木河（简称塔河）地处南疆, 是我国最大的内陆河, 本文以塔河为研究区, 主要关注以下几个科学问题：1）塔河流域站点和区域洪水发生次数的时间演变特征及与极端降水的关系; 2）塔河流域站点和区域洪水发生率的时间非平稳性及不确定性; 3）塔河流域站点和区域洪水过程主要气候影响因子以及可能的概率预测。

1 研究区域和数据

本文选择塔河流域8个水文站点（图1）, 除阿拉尔站外, 其余站点均位于出山口, 较少受到人类活动干扰, 可以有效分析气候变化对洪水发生频率的影响。本文所选主要水文控制站点均有长序列日流量资料, 大部分站点日流量序列时间跨度为1957— 2008年, 数据来源于塔河流域管理局, 部分缺失资料采用多年平均法进行插值。另外, 本文收集了1950— 2000年塔河流域5个地区或州, 即阿克苏地区（简称阿克苏）、克孜勒苏柯尔克孜自治州（简称克州）、喀什地区（简称喀什）、和田地区（简称和田）和巴音郭楞蒙古自治州（简称巴州）的洪水发生次数及发生时间, 数据来源于《中国气象灾害大典— — 新疆卷》^[15]。同时收集了距离每个水文站点最近的气象站点1961— 2010年日降水及日均气温数据（图1）。

塔河流域气象水文过程受大气环流背景重要影响^[16]。Ran等指出SOI（Southern Oscillation Index）和NAO（North Atlantic Oscillation）对新疆气候和水文变化有显著影响^[17]。Kalra等利用NAO、SOI、AMO（Atlantic Multidecadal Oscillation）和PDO（Pacific Decadal Oscillation）对开都河（塔里木河重要的支流之一）径流进行了预测^[18]。因此本文选择冬季（12— 3月）NAO、AO（Arctic Oscillation）、SOI和AMO作为大气环流因子, 分析大气环流对新疆塔河流域洪水发生次数的影响。1950— 2010年月尺度NAO、AO、SOI和AMO值来自http://www.esrl.noaa.gov/psd/data/climateindices/list/.

	Figure Option View Download New Window
	图1 新疆塔河流域水文、气象站点地理分布Fig. 1 Locations of the hydrological stations and meteorological stations across the Tarim River Basin

2 研究方法

2.1 POT（Peak-over-Threshold）抽样技术

洪水样本可以通过最大值抽样和超定量抽样（Peak-over-Threshold, POT）两种方法获得。POT抽样采取超过确定门限值的洪水观测值为样本, 与最大值抽样相比能同时获得洪水发生量级、次数和相应的洪峰出现日期信息, 充分利用观测资料延长洪水样本序列。采用美国水资源协会（USWRC）提出的判别标准对洪峰独立性进行判别^[19]：

$\begin{matrix} \{\begin{matrix} D > 5 + \log (A) \\ Q_{\min} < \frac{3}{4} \min (Q_{1}, Q_{2}) \end{matrix} \end{matrix}$ （1）

式中：D为连续两个洪峰的间隔时间（d）; A为流域面积（km²）; Q₁和Q₂分别为连续两个洪峰的量级（m³/s）。通过超定量样本均值法（MET, 超定量样本超过部分均值是门限值的线性函数）和分散指数法（DI, 门限值的选择应该使样本分散指数位于合适的置信区间）确定门限值区间, 结合年平均洪水发生次数（MnT）, 选择满足平均发生次数在2.4~3.0区间的较大门限值作为阈值^[20]。上述对于极端洪水发生次数的抽样方法同样适用于极端降水次数的抽样。

2.2 非参数洪水发生率估计方法

核估计是用来平滑POT序列点过程数据的一种非参数方法。对于点过程数据密度的估计, 例如时间依赖性的极端事件发生率 $\begin{matrix} λ (t) \end{matrix}$ 的计算如下^{[21, 22]}：

$\begin{matrix} λ (t) = h^{- 1} \overset{m}{\sum_{i = 1}} K (\frac{t - T_{i}}{h}) \end{matrix}$ （2）

式中： $\begin{matrix} T_{i} \end{matrix}$ 为第 $\begin{matrix} i \end{matrix}$ 场洪水发生的时间（d）; $\begin{matrix} m \end{matrix}$ 为POT抽样的洪水个数; $\begin{matrix} K (∙) \end{matrix}$ 为核函数; $\begin{matrix} h \end{matrix}$ 为核函数的窗宽。Gaussian核函数是应用最广泛的核函数, 能够有效利用傅里叶空间并对极端事件发生率 $\begin{matrix} λ (t) \end{matrix}$ 产生一个平滑的估计^{[21, 22]}：

$\begin{matrix} K (y) = \frac{1}{\sqrt{2 π}} \exp (- \frac{y^{2}}{2}) \end{matrix}$ （3）

式中： $\begin{matrix} y = \frac{t - T_{i}}{h} \end{matrix}$ 。极端事件发生率 $\begin{matrix} λ (t) \end{matrix}$ 表示在给定的时间 $\begin{matrix} t \end{matrix}$ , 平均每天超过阈值的极端事件发生次数, 单位为d^-1。由于洪水发生次数常常以年尺度为单位, 因此将洪水发生率 $\begin{matrix} λ (t) \end{matrix}$ 乘以365.25, 表征意义为：给定的时间 $\begin{matrix} t \end{matrix}$ , 平均每年超过阈值的洪水发生次数。

POT抽样数据的时间区间为 $\begin{matrix} [t_{1}, t_{m}] \end{matrix}$ , 由于不存在区间以外的数据, 在进行 $\begin{matrix} λ (t) \end{matrix}$ 的计算时, 往往会低估在边界附近的 $\begin{matrix} λ (t) \end{matrix}$ 。因此采取产生“ 虚拟数据（Pseudo Data）” 的方法来有效减小边界处的估计误差。“ 映射” 方法作为一种直接有效的方法用来产生“ 虚拟数据” ^[21]： $\begin{matrix} pT \end{matrix}$ 为POT抽样数据的时间区间 $\begin{matrix} [t_{1}, t_{m}] \end{matrix}$ 边界之外的“ 虚拟数据” ; 在时间区间 $\begin{matrix} [t_{1}, t_{m}] \end{matrix}$ 的左边, 对于 $\begin{matrix} t < t_{1} \end{matrix}$ , $\begin{matrix} pT [i] = t_{1} - [T_{i} - t_{1}] \end{matrix}$ ; 同理对于边界右边数据（ $\begin{matrix} t > t_{m} \end{matrix}$ ）的延长采取同样的方式。延长后的数据长度是延长前数据长度的1.5倍。用延长后的数据估计 $\begin{matrix} λ (t) \end{matrix}$ 的计算过程如下：

$\begin{matrix} λ (t) = h^{- 1} \overset{m^{*}}{\sum_{i = 1}} K (\frac{t - T_{i}^{*}}{h}) \end{matrix}$ （4）

式中： $\begin{matrix} T_{i}^{*} \end{matrix}$ 为延长后序列的第 $\begin{matrix} i \end{matrix}$ 场洪水发生的时间（d）, $\begin{matrix} m^{*} \end{matrix}$ 为延长后序列的样本长度。在 $\begin{matrix} λ (t) \end{matrix}$ 的估计中窗宽 $\begin{matrix} h \end{matrix}$ 的选择是一个重要的问题。窗宽 $\begin{matrix} h \end{matrix}$ 选择太小, 则随机性影响太大, 产生极不规则的形状; 窗宽 $\begin{matrix} h \end{matrix}$ 选择太大, 则过度平滑, 淹没了密度的细节地方。采用交叉验证的方法确定窗宽 $\begin{matrix} h \end{matrix}$ ^[22]。为了分析 $\begin{matrix} λ (t) \end{matrix}$ 年际间的演变规律, 去除年内季节性变化, 窗宽 $\begin{matrix} h \end{matrix}$ 的取值应该大于365.25 d。用Bootstrap技术确定极端事件发生率 $\begin{matrix} λ (t) \end{matrix}$ 的置信区间^[21]。

2.3 泊松回归

基于 $\begin{matrix} T_{ij} \end{matrix}$ （第 $\begin{matrix} i \end{matrix}$ 年第 $\begin{matrix} j \end{matrix}$ 场极端事件发生的时间）, 则极端事件每年发生个数为：

$\begin{matrix} N_{i} (t) = \overset{n_{i}}{\sum_{j = 1}} 1 (T_{ij} \leq t) \end{matrix}$ （5）

$\begin{matrix} t \end{matrix}$ 的取值范围为[0, 365或366]。极端事件发生次数序列常常符合泊松分布：

$\begin{matrix} P (N_{i} = k |Λ_{i}) = \frac{e^{- Λ_{i}} Λ_{i}^{k}}{k!} (k = 0, 1, 2, \dots) \end{matrix}$ （6）

式中： $\begin{matrix} Λ_{i} \end{matrix}$ 是一个非负随机变量。泊松回归的响应变量是发生次数。在泊松回归中, $\begin{matrix} Λ_{i} \end{matrix}$ 与协变量的关系如下：

$\begin{matrix} Λ_{i} = \exp [β_{0} + β_{1} h_{1} (x_{1, i}) + β_{2} h_{2} (x_{2, i}) + \dots + β_{n} h_{n} (x_{n, i})] \end{matrix}$ （7）

式中： $\begin{matrix} (x_{1, i}, x_{2, i}, \dots, x_{n, i}) \end{matrix}$ 是协变量向量, 例如大气环流因子（本文为冬季NAO、AO、SOI和AMO）; $\begin{matrix} (β_{0}, β_{1}, \dots, β_{n}) \end{matrix}$ 为协变量系数向量。GAMLSS（Generalized Additive Models for Location, Scale and Shape）模型被广泛用来构建响应变量和协变量之间的回归关系, 并识别最显著的协变量因子^{[23, 24, 25]}。

本文考虑4种形式的协变量： $\begin{matrix} Λ_{i} \end{matrix}$ 为不变的常量（稳定性模型Model 0）; $\begin{matrix} Λ_{i} \end{matrix}$ 以时间 $\begin{matrix} t \end{matrix}$ 为协变量, 随时间 $\begin{matrix} t \end{matrix}$ 而变化（非稳定性模型Model 1）; $\begin{matrix} Λ_{i} \end{matrix}$ 以大气环流因子（冬季NAO、AO、SOI和AMO）为协变量（非稳定性模型Model 2）; $\begin{matrix} Λ_{i} \end{matrix}$ 以年总降水量、极端降水发生次数（日降水序列的POT抽样序列）和冬季（12— 3月）平均日平均温度为协变量（Model 3）。三次立方样条函数被用来作为平滑函数 [ $\begin{matrix} h_{n} (x_{n, i}) \end{matrix}$ ], AIC（Akaike Information Criterion）准则用来判别最优模型和最显著协变量, Filliben系数用来判断AIC识别的最优模型的拟合质量^{[23, 24, 25]}。

3 研究结果

3.1 基于POT抽样的数据分析

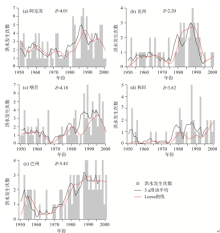
通过POT抽样技术对日流量和日降水序列进行抽样, 可以获取极端事件发生时间序列和每年极端事件发生次数序列。通过5 a滑动平均和Loess函数对极端事件发生次数序列分别进行平滑和拟合, 分析极端事件发生次数的变化特征。同时用修正Mann-Kendall法对5 a滑动平均序列进行趋势分析。图2给出了洪水发生次数序列的时间变化特征。塔河流域几乎所有水文站点洪水发生次数均有两个高峰期：1960年左右和1990年左右。所有水文站点在1970年代和1980年代洪水发生次数多为2或3次。由Loess曲线可知, 进入21世纪后, 除大山口站, 其余各站洪水发生次数均有不同程度的回落趋势。就整个观测时期来看, 同古孜洛克站、协和拉站和阿拉尔站洪水发生次数呈下降趋势, 其中协和拉站和阿拉尔站呈显著下降趋势; 其余各站呈上升趋势, 除喀群站外均呈显著上升趋势。

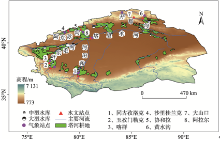	Figure Option View Download New Window
	图1 新疆塔河流域水文、气象站点地理分布Fig. 1 Locations of the hydrological stations and meteorological stations across the Tarim River Basin

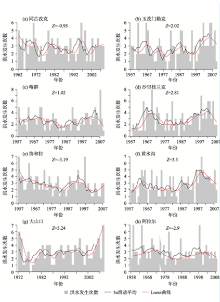	Figure Option View Download New Window
	图2 新疆塔河流域各水文站点极端洪水发生次数时间分布注：黑色线为5 a滑动平均值, Z值为5 a滑动平均值的MK统计值, Z绝对值大于1.96表示趋势具有显著性。红色线为Loess函数拟合值, 自由度f = 0.2。Fig. 2 Temporal changes of flooding frequency of the Tarim River Basin

通过统计覆盖整个塔河流域5个州实际发生的洪水次数, 研究区域洪水发生次数的时间演变规律见图3。与水文站点洪水发生次数一致, 阿克苏地区、克州和喀什地区洪水发生次数具有相似的时间演变特征：分别在1960年和1990年左右达到顶峰; 从1980年开始洪水发生次数有一个迅猛增长过程, 洪水集中大量发生, 其规模是1980年以前的2倍左右; 从1995年开始有一个回落过程。和田地区在1980年以前洪水发生次数较少, 甚至多数年份没有发生洪水, 但是1980年以后几乎每年都有洪水发生, 在1990年左右达到顶峰, 洪水发生次数一年最高有5次之多。区域洪水次数增加数量和上升速度均明显高于和快于站点洪水, 对气候变化的响应更加敏感。巴州洪水发生次数在1955年和1988年左右分别达到顶峰; 从1960年开始直到1988年洪水发生次数有一个快速上升过程, 1988年达到顶峰后一直在高位震荡, 没有出现回落。就整个记录时期（1950— 2000年）来看, 覆盖塔河流域5个州的洪水发生次数均呈显著增加趋势。塔河流域洪水发生次数已经呈现非平稳性过程, 将对洪水资源管理和防洪提出新的挑战。

	Figure Option View Download New Window
	图3 新疆塔河流域各区域极端洪水发生次数时间分布Fig. 3 Temporal changes of flooding frequency in the subregions of the Tarim River Basin

3.2 洪水发生率的非平稳性特征

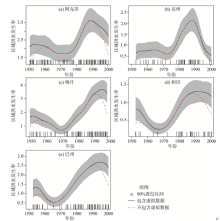
基于从日流量和日降水数据通过POT抽样获取极端事件发生时间数据, 然后用核估计和Bootstrap技术估计极端事件发生率λ (t)及相应的不确定性（置信区间）（图4）。由图4看出, 洪水发生率呈现明显的年代际变化特征, 例如玉孜门勒克站进入21世纪后, 洪水发生率达到最高峰, 甚至高于1990年的90%置信区间的上限。除同古孜洛克站洪水发生率表现较为平稳外, 其余站点均表现出较强的非平稳的泊松过程：1）洪水发生率从1990年左右开始, 均有一个上升过程, 并达到峰值, 意味着洪水发生频率更高, 强度更大; 2）除大山口站, 其余站点洪水发生率在1970年左右达到一个小峰值, 然后下降直到1980年左右降到最低; 3）所有站点在2000年以后洪水发生率开始下降, 意味着洪水发生频率回落, 强度降低。

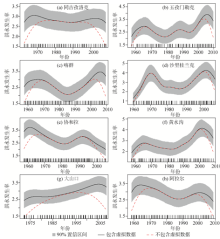	Figure Option View Download New Window
	图4 新疆塔河流域各水文站点洪水发生率时间分布Fig. 4 Trends of flooding frequency at the hydrological stations in the Tarim River Basin

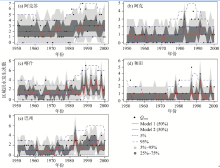
从区域洪水发生率来看, 其非平稳性更加显著（图5）。覆盖整个塔河流域的5个区域洪水发生率的时间变化特征具有非常高的相似性：1）从1950— 1970年处于下降趋势, 到1970年左右洪水发生率达到最低值, 意味着洪水发生频率达到记录以来的最低水平, 洪水活动的强度最低; 2）从1970年左右, 洪水发生率有一个陡然升高的过程, 一直持续到1995年左右, 并在1995年左右达到峰值, 意味着洪水发生频率达到记录以来的最高值, 强度最强; 从1995年开始, 洪水发生率又开始回落, 洪水发生频率减弱。由于5个区域均表现相似的特征, 可以认为整个塔河流域1950— 2000年洪水发生率具有跟上述5个区域相同的过程。

	Figure Option View Download New Window
	图5 新疆塔河流域各区域洪水发生率时间分布Fig. 5 Trends of flooding frequency in the subregions of the Tarim River Basin

3.3 洪水发生次数与气候变化之间的关系

构建3种GAMLSS模型分析水文站点洪水发生次数和协变量之间的关系：非平稳性模型（Model 1、2和3）。表1为3种GAMLSS模型的AIC值、Filliben系数及与协变量之间的函数关系等信息。从表1看出, 在Model 2中, AMO是最优协变量站点最多的气候指标, 共有4个站点, 其次是AO, 共有3个站点; 在Model 3中, 年平均降水量和冬季日平均温度均是最优协变量站点最多的气候因子, 均分别有4次。由AIC值可知, 仅以时间为协变量的Model 1的AIC在大部分站点均高于平稳性模型（AIC值略）, 说明Model 1在描述洪水发生次数方面较差。在大部分站点, 分别以大气环流因子及降水和气温指标为协变量的Model 2和3的AIC值小于平稳性模型, 尤其是考虑降水和气温指标的Model 3, 其AIC值明显低于平稳性模型, 表明考虑物理成因协变量能增强模型模拟洪水发生次数的能力。从Filliben系数来看, 所有模型的Filliben系数均高于0.95, 说明模型拟合质量满足分析要求。

表1 3种不同的GAMLSS模型对站点洪水发生次数序列的拟合信息 Table 1 Goodness-of-fit results of three GAMLSS models for flooding frequency

站点	Model 1			Model 2				Model 3
站点	AIC		Filliben		AIC	$\begin{matrix} Λ_{i} \end{matrix}$	Filliben	AIC	$\begin{matrix} Λ_{i} \end{matrix}$	Filliben
同古孜洛克	174	0.99		165^*	AO+AMO	0.98		169	x₃	0.99
玉孜门勒克	205	0.99		203	AMO	0.99		186^*	x₁	1.00
喀群	188	0.99		182	AMO	0.98		174^*	x₃	0.98
沙里桂兰克	197	0.99		200	SOI	0.99		183^*	cs(x₂)	0.99
协和拉	181	0.99		182	AO	0.98		162^*	x₂	0.99
黄水沟	197	0.99		195	AMO	0.99		169^*	x₂+x₃	1.00
大山口	139	0.98		139	AO	0.99		138^*	x₃	0.99
阿拉尔	186	0.97		179	NAO+SOI	0.99		168^*	x₂	0.96

注：AIC值为最终确定的最优模型的AIC值; Filliben系数用来判别最优模型的拟合效果（Filliben系数大于0.95, 表明模拟拟合效果较好）; cs()表示三次立方样条函数, 没有cs表示线性关系; 加黑数值表示AIC小于或等于Model 0; * 表示AIC值在4种模型中最小; x₁为极端降水发生次数, x₂为平均年降水量, x₃为冬季日平均温度。

表1 3种不同的GAMLSS模型对站点洪水发生次数序列的拟合信息 Table 1 Goodness-of-fit results of three GAMLSS models for flooding frequency

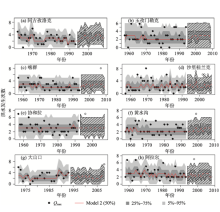
从图6看出, 在Model 1中, 从1990年左右开始, 洪水发生次数有一个阶梯上升的过程; 但是大部分站点在1990年前洪水发生次数分位数（5%和95%）是一条较为平稳的直线, 较难反映洪水发生次数的随机过程。将协变量大气环流因子纳入到模型中（Model 2）则能明显改善这种情况, 更充分地抓住洪水发生次数的波动和离散特征。例如同古孜洛克站, 洪水发生次数从1990年开始5%~95%处于波动上升, 而时间为协变量模型Model 0则一直为平稳性直线, 无法体现出洪水发生次数的起伏状态。Model 2同时反映出最显著识别因子对洪水发生次数的拟合有非常好的效果。由于冬季大气环流因子（12— 3月）往往可以先于当年洪水发生时间（一般为5— 9月）, 因此可以基于这种较好的拟合效果和回归关系, 用冬季大气环流因子对当年洪水发生次数做一个概率预测, 用作防洪减灾的指导。

	Figure Option View Download New Window
	图6 基于GAMLSS模型分别以时间（Model 1）和大气环流因子（Model 2）为协变量拟合各水文站点洪水发生次数序列Fig. 6 Modeled flooding frequency by using GAMLSS with time (Model 1) and climate indices (Model 2) as covariate

Model 3对洪水发生次数的拟合效果相比Model 2进一步具有波动性和离散性（图7）。另外, Model 3的AIC值是4种模型中最小的, 进一步说明了Model 3更充分地抓住了洪水发生次数序列的时间变化特征（表2）。尤其对于玉孜门勒克站、沙里桂兰克站及黄水沟站, Model 3对洪水发生次数序列的波动特征反映得更充分, 例如1970年代洪水活动加强, 达到一个波峰, 1990年代洪水活动达到一个更强的水平。大气环流因子一般更直接影响降水和气温, 从而间接影响洪水过程, 而降水和气温能够直接影响洪水发生。因此洪水发生过程对降水和气温的变化更敏感。基于降水和气温对洪水发生次数拟合具有较好的效果。

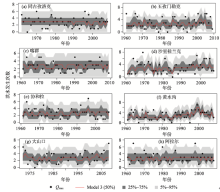	Figure Option View Download New Window
	图7 基于GAMLSS模型以降水和气温指标为协变量（Model 3）拟合各水文站点洪水发生次数序列Fig. 7 Modeled flooding frequency by using GAMLSS with precipitation and temperature (Model 3) as covariate

对于区域洪水发生次数, 本文则构建了两种GAMLSS模型（除去降水和气温为协变量的Model 3）分析区域洪水发生次数序列与协变量之间的关系。同表1一致, 表2综合了两种GAMLSS模型的拟合AIC值、Filliben系数及与协变量之间的函数关系等信息。从表2可以看出, 在Model 2中NAO和SOI是5个区域最显著的协变量, AO和AMO则对区域洪水发生次数没有显著的影响。从AIC值来看, 不论是以时间为协变量的Model 1还是以气候指标为协变量的Model 2, 两者AIC值均明显比平稳性模型小（AIC值略）, 说明区域洪水发生次数呈现无可争议的非平稳性。从Filliben系数来看（表2）, 所有模型的Filliben系数均高于0.95, 说明模型拟合质量满足分析要求。

表2 3种不同的GAMLSS模型对站点洪水发生次数序列的拟合信息 Table 2 Goodness-of-fit results of three GAMLSS models for flooding frequency

从图8看出, 在Model 1中, 时间为协变量的模型能够反映区域洪水发生次数从1980年代开始有一个阶梯上升过程, 然后在1995年之后有一个阶梯下降的趋势, 尤其是95%分位数线。对于Model 2, 区域洪水发生次数无论是50%分位数线还是95%分位数线均是剧烈地波动, 在波动中上升。尤其是95%分位数线, 能够有效地抓住极端值的变化特征。NAO和SOI是仅有的两个对区域洪水发生次数有显著影响的气候因子, 能够有效反映区域洪水发生次数的变化特征, 有利于对区域洪水发生次数做短期预测。

	Figure Option View Download New Window
	图8 基于GAMLSS模型分别以时间（Model 1）和大气环流因子（Model 2）为协变量拟合各区域洪水发生次数序列Fig. 8 Modeled flood frequency in the subregions of the Tarim River Basin by using GAMLSS with time (Model 1) and climate index (Model 2) as covariate

3.4 非平稳性模型的预测效果

在洪水管理中, 如果能够对洪水有一定程度的预测, 将有效地提升人类社会应对洪水的能力。在通过GAMLSS模型建立洪水发生次数与协变量之间的关系后, 基于这种关系, 用协变量就能够对洪水发生次数进行概率分位数预测。以大气环流因子为协变量为例, 分别预测实测期后15 a水文站点和区域洪水发生次数的分位数（图9）。从图9看出, 用水文站点前期实测洪水发生次数识别最显著的大气环流因子, 基于已经建立的非平稳性模型, 能够很好地抓住后15 a洪水发生次数的分位数特征。所有水文站点预测的后15 a分位数（5%~95%分位数）均能反映1990年代以来洪水发生次数加强、呈上升趋势的特征。同时能够体现出洪水发生次数的波动性和离散性特征。而且5%~95%分位数区间几乎能包含所有实测的洪水发生次数序列, 表明基于气候指标的非平稳性模型能够对洪水发生次数提供一个较好的预测效果。

	Figure Option View Download New Window
	图9 各站点洪水发生次数以大气环流因子为协变量（Model 2）概率预测后15 a洪水发生次数分位数图Fig. 9 Predicted flooding frequency in the 15 years since mid-1990s by using Model 2 with climate index as the covariate

4 结论

本文采用POT抽样获得了洪水和极端降水事件发生时间和发生次数两种要素信息, 采用核估计和Bootstrap技术分别评价极端事件发生时间的非平稳性和不确定性, 并用GAMLSS模型建立极端事件发生次数与时间、大气环流因子和降水、气温指标等协变量之间的模型并识别最显著的协变量。从中得出一些有意义的结论：

1）塔河流域几乎所有水文站点洪水发生次数存在两个高峰期：1960年左右和1990年左右。在两个峰期之间, 洪水发生次数多为2或3次。覆盖塔河流域5个区域的洪水发生次数变化过程出现的两个峰期与水文站点基本吻合, 但是区域洪水发生次数在1980年之后的增加速率和增加次数远高于水文站点。极端降水发生次数过程尤其在1990年代与水文站点有较高的相似性。

2）塔河流域水文站点洪水发生率已经出现不均匀泊松过程, 即洪水发生率是非平稳性的, 例如玉孜门勒克、沙里桂兰克及黄水沟站等。区域洪水发生率非平稳性过程更显著。水文站点和区域洪水发生率均具有相似的变化特征：从1990年左右持续上升并达到峰值, 意味着洪水发生频率更高, 强度更大。区域洪水发生率在这一时期的上升速率远高于水文站点。

3）以大气环流因子或降水、气温指标为协变量的模型, 均能很好地抓住洪水发生次数的变化特征。对于水文站点洪水发生次数, 冬季AMO和AO是最显著的影响因子; 对于区域洪水发生次数, 冬季NAO和SOI是最显著的影响因子。从AIC值来看, 相比大气环流因子, 洪水发生次数对降水和气温指标更敏感, 拟合效果更好。

4）考虑物理影响因子（例如大气环流因子、降水、气温等）的非平稳性模型在对洪水发生次数进行预测时, 往往具有较好的预测效果, 能够充分抓住洪水发生次数序列的离散性和波动性特征及极端值的变化特征。这一性质将对以后的洪水管理具有重要的预测和指导价值。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	顾西辉, 张强, 陈晓宏. 中国降水及流域径流均匀度时空特征及影响因子研究[J]. 自然资源学报, 2015, 30(10): 1714-1724. [GU X H, ZHANG Q, CHEN X H. Spatiotemporal patterns ofuniformity of precipitation and runoff over China and related influencing factors. Journal of Natural Resources, 2015, 30(10): 1714-1724. ] [本文引用:1]
[2]	孙莉英, 倪晋仁, 蔡强国, 等. 中国洪水灾害风险县(市)统计分布特征研究[J]. 自然资源学报, 2013, 28(3): 391-401. [SUN L Y, NI J R, CAI Q G, et al. Statistical distribution characteristics of counties and cities for flood risk in China. Journal of Natural Resources, 2013, 28(3): 391-401. ] [本文引用:1]
[3]	MILLY P C D, BETANCOURT J, FALKENMARK M, et al. Stationarity is dead: Whither water management?[J]. Science, 2008, 319(5863): 573-574. [本文引用:1]
[4]	顾西辉, 张强, 刘剑宇, 等. 变化环境下珠江流域洪水频率变化特征、成因及影响(1951—2010年)[J]. 湖泊科学, 2014, 26(5): 661-670. [GU X H, ZHANG Q, LIU J Y, et al. Characteristics, causes and impacts of the changes of the flood frequency in the Pearl River drainage basin from 1951 to 2010. Journal of Lake Sciences, 2014, 26(5): 661-670. ] [本文引用:1]
[5]	顾西辉, 张强, 陈晓宏, 等. 气候变化和人类活动联合影响下东江流域非一致性洪水频率[J]. 热带地理, 2014, 34(6): 746-757. [GU X H, ZHANG Q, CHEN X H, et al. Nonstationary flood frequency analysis considering the combined effects of climate change and human activities in the East River Basin. Tropical Geography, 2014, 34(6): 746-757. ] [本文引用:1]
[6]	顾西辉, 张强. 考虑水文趋势影响的珠江流域非一致性洪水风险分析[J]. 地理研究, 2014, 33(9): 1680-1693. [GU X H, ZHANG Q. Non-stationary flood risk analysis in Pearl River Basin, considering the impact of hydrological trends. Geographical Research, 2014, 33(9): 1680-1693. ] [本文引用:1]
[7]	冯平, 李新. 基于Copula函数的非一致性洪峰洪量的联合分析[J]. 水利学报, 2013, 44(10): 1137-1147. [FENG P, LI X. Bivariate frequency analysis of non-stationary flood time series based on Copula methods. Journal of Hydraulic Engineering, 2013, 44(10): 1137-1147. ] [本文引用:1]
[8]	施雅风, 沈永平, 胡汝骥. 西北气候由暖干向暖湿转型的信号、影响和初步探讨[J]. 冰川冻土, 2002, 24(3): 219-226. [SHI Y F, SHEN Y P, HU R J. Preliminary study on signal, impact and foreground of climatic shift from Warm-Dry to Warm-Humid in Northwest China. Journal of Glaciology and Geocryology, 2002, 24(3): 219-226. ] [本文引用:1]
[9]	冯思, 黄云, 许有鹏. 全球变暖对新疆水循环影响分析[J]. 冰川冻土, 2006, 28(4): 500-505. [FENG S, HUANG Y, XU Y P. Impact of global warming on the water cycle in Xinjiang region. Journal of Glaciology and Geocryology, 2006, 28(4): 500-505. ] [本文引用:1]
[10]	慈晖, 张强, 张江辉, 等. 1961—2010年新疆极端降水过程时空特征[J]. 地理研究, 2014, 33(10): 1881-1891. [CI H, ZHANG Q, ZHANG J H, et al. Spatiotemporal variations of extreme precipitation events within Xinjiang during 1961-2010. Geographical Research, 2014, 33(10): 1881-1891. ] [本文引用:1]
[11]	陈亚宁, 杨青, 罗毅, 等. 西北干旱区水资源问题研究思考[J]. 干旱区地理, 2012, 35(1): 1-9. [CHEN Y N, YANG Q, LUO Y, et al. Ponder on the issues of water resources in the arid region of Northwest China. Arid Land Geography, 2012, 35(1): 1-9. ] [本文引用:1]
[12]	陈亚宁, 徐长春, 杨余辉, 等. 新疆水文水资源变化及对区域气候变化的响应[J]. 地理学报, 2009, 64(11): 1331-1341. [CHEN Y N, XU C C, YANG Y H, et al. Hydrology and water resources variation and its responses to regional climate change in Xinjiang. Acta Geographica Sinica, 2009, 64(11): 1331-1341. ] [本文引用:1]
[13]	王秋香, 崔彩霞, 姚艳丽. 新疆不同区域洪灾受灾面积变化趋势及多尺度分析[J]. 地理学报, 2008, 63(7): 769-779. [WANG Q X, CUI C X, YAO Y L, et al. Variation trends and multi- scale analysis of flood affected area in various regions of Xinjiang. Acta Geographica Sinica, 2008, 63(7): 769-779. ] [本文引用:1]
[14]	姜逢清, 胡汝骥, 杨跃辉. 新疆洪灾时间序列突变及其气候原因分析[J]. 冰川冻土, 2004, 26(6): 674-681. [JIANG F Q, HU R J, YANG Y H. Abrupt change in the time sequences of flood disasters in Xinjiang and its possible climatic reasons. Journal of Glaciology and Geocryology, 2004, 26(6): 674-681. ] [本文引用:1]
[15]	史玉光, 温克刚. 中国气象灾害大典——新疆卷 [M]. 北京: 气象出版社, 2006. [SHI Y G, WEN K G. China’s Meteorological Disaster Ceremony—Volume in Xinjiang. Beijing: China Meteorological Press, 2006. ] [本文引用:1]
[16]	陈亚宁, 李稚, 范煜婷, 等. 西北干旱区气候变化对水文水资源影响研究进展[J]. 地理学报, 2014, 69(9): 1295-1304. [CHEN Y N, LI Z, FAN Y T, et al. Research progress on the impact of climate change on water resources in the arid region of Northwest China. Acta Geographica Sinica, 2014, 69(9): 1295-1304. ] [本文引用:1]
[17]	RAN M, ZHANG C, ZHAO F. Climatic and hydrological variations during the past 8000 years in Northern Xinjiang of China and the associated mechanisms[J]. Quaternary International, 2015, 358: 21-34. [本文引用:1]
[18]	KALRA A, LI L H, LI X M, et al. Improving streamflow forecast lead time using oceanic-atmospheric oscillations for Kaidu River Basin, Xinjiang, China[J]. Journal of Hydrologic Engineering, 2013, 18(8): 1031-1040. [本文引用:1]
[19]	LANG M, OUARDAB T B M J, BOBEE B. Towards operational guidelines for over-threshold modeling[J]. Journal of Hydrology, 1999, 255(3/4): 103-117. [本文引用:1]
[20]	顾西辉, 张强, 孙鹏, 等. 新疆塔河流域洪水量级、频率及峰现时间变化特征、成因及影响[J]. 地理学报, 2015, 70(9): 1390-1401. [GU X H, ZHANG Q, SUN P, et al. Magnitude, frequency and timing of floods in the Tarim River, Xinjiang: Characteristics, causes and impacts. Acta Geographica Sinica, 2015, 70(9): 1390-1401. ] [本文引用:1]
[21]	MUDELSEE M. Extreme floods in central Europe over the past 500 years: Role of cyclone pathway “ZugstrasseVb”[J]. Journal of Geophysical Research, 2004, 109: D23101. [本文引用:4]
[22]	MUDELSEE M, BORNGEN M, TETZLAFF M, et al. No upward trends in the occurrence of extreme floods in central Europe[J]. Nature, 2003, 425: 166-169. [本文引用:3]
[23]	RIGBY R A, STASINOPOULOS D M. Generalized additive models for location, scale and shape[J]. Applied Statistics, 2005, 54(3): 507-554. [本文引用:2]
[24]	姜聪, 熊立华. 基于 GAMLSS 模型的宜昌站年径流序列趋势分析[J]. 地理学报, 2012, 67(11): 1505-1514. [JIANG C, XIONG L H. Trend analysis for the annual discharge series of the Yangtze River at the Yichang Hydrological Station based on GAMLSS. Acta Geographica Sinica, 2012, 67(11): 1505-1514. ] [本文引用:2]
[25]	顾西辉, 张强, 王宗志. 1951—2010年珠江流域洪水极值序列平稳性特征研究[J]. 自然资源学报, 2015, 30(5): 824-835. [GU X H, ZHANG Q, WANG Z Z. Evaluation on stationarity assumption of annual maximum peak flows during 1951-2010 in the Pearl River Basin. Journal of Natural Resources, 2015, 30(5): 824-835. ] [本文引用:2]

2015

0.0

顾西辉, 张强, 陈晓宏. 中国降水及流域径流均匀度时空特征及影响因子研究[J]. 自然资源学报, 2015, 30(10): 1714-1724.

[GU X

, ZHANG

, CHEN X

. Spatiotemporal patterns ofuniformity of precipitation and runoff over China and related influencing factors. Journal of Natural Resources, 2015, 30(10): 1714-1724. ]

... 全球变暖及其对生态、水资源、人类社会等的影响已引起人们的广泛关注^[1],尤其是在气候暖化影响下,极端水文气象事件（例如洪水和干旱）发生频率与强度有加剧化趋势^[2] ...

2013

0.0

孙莉英, 倪晋仁, 蔡强国, 等. 中国洪水灾害风险县(市)统计分布特征研究[J]. 自然资源学报, 2013, 28(3): 391-401.

[SUN L

, NI J

, CAI Q

, et al. Statistical distribution characteristics of counties and cities for flood risk in China. Journal of Natural Resources, 2013, 28(3): 391-401. ]

2008

0.0

... Milly等^[3,4,5]研究认为,在洪水管理中,洪水过程的平稳性假设受到越来越多的挑战,需要在洪水过程研究中考虑非平稳性问题 ...

2014

0.0

顾西辉, 张强, 刘剑宇, 等. 变化环境下珠江流域洪水频率变化特征、成因及影响(1951—2010年)[J]. 湖泊科学, 2014, 26(5): 661-670.

[GU X

, ZHANG

, LIU J

, et al. Characteristics, causes and impacts of the changes of the flood frequency in the Pearl River drainage basin from 1951 to 2010. Journal of Lake Sciences, 2014, 26(5): 661-670. ]

... Milly等^[3,4,5]研究认为,在洪水管理中,洪水过程的平稳性假设受到越来越多的挑战,需要在洪水过程研究中考虑非平稳性问题 ...

2014

0.0

顾西辉, 张强, 陈晓宏, 等. 气候变化和人类活动联合影响下东江流域非一致性洪水频率[J]. 热带地理, 2014, 34(6): 746-757.

[GU X

, ZHANG

, CHEN X

, et al. Nonstationary flood frequency analysis considering the combined effects of climate change and human activities in the East River Basin. Tropical Geography, 2014, 34(6): 746-757. ]

... Milly等^[3,4,5]研究认为,在洪水管理中,洪水过程的平稳性假设受到越来越多的挑战,需要在洪水过程研究中考虑非平稳性问题 ...

2014

0.0

顾西辉, 张强. 考虑水文趋势影响的珠江流域非一致性洪水风险分析[J]. 地理研究, 2014, 33(9): 1680-1693.

[GU X

, ZHANG

. Non-stationary flood risk analysis in Pearl River Basin, considering the impact of hydrological trends. Geographical Research, 2014, 33(9): 1680-1693. ]

... 顾西辉等考虑了洪峰序列中的趋势性在洪水风险分析中的影响^[6] ...

2013

0.0

冯平, 李新. 基于Copula函数的非一致性洪峰洪量的联合分析[J]. 水利学报, 2013, 44(10): 1137-1147.

[FENG

, LI

. Bivariate frequency analysis of non-stationary flood time series based on Copula methods. Journal of Hydraulic Engineering, 2013, 44(10): 1137-1147. ]

... 冯平等^[7]用Copula函数构建洪峰和洪量的非一致性频率分析模型 ...

2002

0.0

施雅风, 沈永平, 胡汝骥. 西北气候由暖干向暖湿转型的信号、影响和初步探讨[J]. 冰川冻土, 2002, 24(3): 219-226.

[SHI Y

, SHEN Y

, HU R

. Preliminary study on signal, impact and foreground of climatic shift from Warm-Dry to Warm-Humid in Northwest China. Journal of Glaciology and Geocryology, 2002, 24(3): 219-226. ]

... 施雅风等认为西北地区气候可能由暖干转向暖湿^[8] ...

2006

0.0

冯思, 黄云, 许有鹏. 全球变暖对新疆水循环影响分析[J]. 冰川冻土, 2006, 28(4): 500-505.

[FENG

, HUANG

, XU Y

. Impact of global warming on the water cycle in Xinjiang region. Journal of Glaciology and Geocryology, 2006, 28(4): 500-505. ]

... 冯思等进一步指出气温上升导致水循环加速,进而引起新疆地区降水量增加^[9] ...

2014

0.0

慈晖, 张强, 张江辉, 等. 1961—2010年新疆极端降水过程时空特征[J]. 地理研究, 2014, 33(10): 1881-1891.

[CI

, ZHANG

, ZHANG J

, et al. Spatiotemporal variations of extreme precipitation events within Xinjiang during 1961-2010. Geographical Research, 2014, 33(10): 1881-1891. ]

With the development of global climate change, extreme climate events have drawn attention of worldwide researchers not only due to their direct impact on socio-economy, but also as climate change indicators. Human and natural systems have been affected by extreme climate events to a great extent. The main objective of our study is to detect the possible changes and intensity, tendency and frequency of extreme climate events. Xinjiang is located in the inland China, where the climate is arid to semi-arid. Xinjiang is therefore highly vulnerable to climate variability, and a better understanding of changes in extreme precipitation events plays an increasingly role in the arrangement of agricultural production and the process of agricultural planning. Fourteen extreme precipitation indices have been selected and spatiotemporal patterns of extreme precipitation events have been analyzed based on daily precipitation data from 50 stations covering the period of 1961-2010 using statistical methods. The results indicate that precipitation amount is in an upward trend with increasing precipitation intensity and precipitation frequency. With the increase of precipitation, evident decrease of CDD can be found and increasing trend can be identified by RR1, RR5, RR10, R95P, Rx1day and Rx5day. This result show obvious wetting tendency in Xinjiang. However, different time periods are dominated by different changing properties of precipitation regimes. With smaller variability and higher stability, precipitation amount level during 1960-1970s is lower. The period of 1980-1990s can be taken as the transitional period characterized by abrupt increase of precipitation amount and lower stability, and according to unsteady precipitation variations in recent years, higher precipitation variability can be found after the 1990s. Spatially, increasing and decreasing trends of precipitation variations alternate in eastern Xinjiang with small amplitudes; however, evident increase of precipitation can be found in the northern, southern and the entire Xinjiang region. Alteration of precipitation variations was found mainly in 1986 and 2009. After occurrence of precipitation alteration, strong precipitation processes are subject to higher variability and moderate changing characteristics are found in weak precipitation processes. This study will be of great merits in terms of development of human understanding of regional responses of hydrological cycle to climate changes in Xinjiang.

1. Department of Water Resources and Environment, Sun Yat-sen University, Guangzhou 510275, China; 2. Key Laboratory of Water Cycle and Water Security in Southern China of Guangdong High Education Institute, Sun Yat-sen University, Guangzhou 510275, China; 3. Xinjiang Research Institute of Water Resources and Hydropower, Xinjiang 830049, China.

采用新疆50个气象测站1961-2010年逐日降水资料,选用14个极端降水指数探讨新疆极端降水事件的发生与变化。结果表明：无论平均降水过程还是极端降水过程,均能反映新疆明显的湿润化趋势。伴随降水量的增加,降水强度及降水频率均增大,除CDD变化表现为下降趋势外,其他指数变化均呈上升趋势。分析各极端降水指数序列变化,20世纪60-70年代年际变化幅度小,稳定性好;80-90年代年际差异大,稳定性差;新疆东部各极端降水指数上升与下降趋势小幅交替出现,而北疆、南疆及全疆极端指数序列则呈明显且单一的上升趋势。各极端降水指数最大概率变异年为1986年、2009年;降水变异后,新疆弱降水过程变化不明显,但强降水过程变幅增大,易导致洪旱灾害等极端气象水文事件的发生。

... 慈晖等采用多个极端降水指标分析了新疆极端降水过程,发现强降水过程变幅增大,易导致洪旱灾害等极端气象水文事件发生^[10] ...

2012

0.0

陈亚宁, 杨青, 罗毅, 等. 西北干旱区水资源问题研究思考[J]. 干旱区地理, 2012, 35(1): 1-9.

[CHEN Y

, YANG

, LUO

, et al. Ponder on the issues of water resources in the arid region of Northwest China. Arid Land Geography, 2012, 35(1): 1-9. ]

... 新疆降水过程的变化导致洪涝灾害在近几十年呈显著上升趋势^[11] ...

2009

0.0

陈亚宁, 徐长春, 杨余辉, 等. 新疆水文水资源变化及对区域气候变化的响应[J]. 地理学报, 2009, 64(11): 1331-1341.

[CHEN Y

, XU C

, YANG Y

, et al. Hydrology and water resources variation and its responses to regional climate change in Xinjiang. Acta Geographica Sinica, 2009, 64(11): 1331-1341. ]

... 有研究表明：新疆洪水发生频次增加,洪峰流量增大^[12],并且洪灾导致的受灾面积也呈显著增加趋势^[13,14] ...

2008

0.0

王秋香, 崔彩霞, 姚艳丽. 新疆不同区域洪灾受灾面积变化趋势及多尺度分析[J]. 地理学报, 2008, 63(7): 769-779.

[WANG Q

, CUI C

, YAO Y

, et al. Variation trends and multi- scale analysis of flood affected area in various regions of Xinjiang. Acta Geographica Sinica, 2008, 63(7): 769-779. ]

... 有研究表明：新疆洪水发生频次增加,洪峰流量增大^[12],并且洪灾导致的受灾面积也呈显著增加趋势^[13,14] ...

2004

0.0

姜逢清, 胡汝骥, 杨跃辉. 新疆洪灾时间序列突变及其气候原因分析[J]. 冰川冻土, 2004, 26(6): 674-681.

[JIANG F

, HU R

, YANG Y

. Abrupt change in the time sequences of flood disasters in Xinjiang and its possible climatic reasons. Journal of Glaciology and Geocryology, 2004, 26(6): 674-681. ]

... 有研究表明：新疆洪水发生频次增加,洪峰流量增大^[12],并且洪灾导致的受灾面积也呈显著增加趋势^[13,14] ...

2006

0.0

... 新疆卷》^[15] ...

2014

0.0

陈亚宁, 李稚, 范煜婷, 等. 西北干旱区气候变化对水文水资源影响研究进展[J]. 地理学报, 2014, 69(9): 1295-1304.

[CHEN Y

, LI

, FAN Y

, et al. Research progress on the impact of climate change on water resources in the arid region of Northwest China. Acta Geographica Sinica, 2014, 69(9): 1295-1304. ]

... 塔河流域气象水文过程受大气环流背景重要影响^[16] ...

2015

0.0

... Ran等指出SOI（Southern Oscillation Index）和NAO（North Atlantic Oscillation）对新疆气候和水文变化有显著影响^[17] ...

2013

0.0

... Kalra等利用NAO、SOI、AMO（Atlantic Multidecadal Oscillation）和PDO（Pacific Decadal Oscillation）对开都河（塔里木河重要的支流之一）径流进行了预测^[18] ...

1999

0.0

... 采用美国水资源协会（USWRC）提出的判别标准对洪峰独立性进行判别^[19]： ...

2015

0.0

顾西辉, 张强, 孙鹏, 等. 新疆塔河流域洪水量级、频率及峰现时间变化特征、成因及影响[J]. 地理学报, 2015, 70(9): 1390-1401.

[GU X

, ZHANG

, SUN

, et al. Magnitude, frequency and timing of floods in the Tarim River, Xinjiang: Characteristics, causes and impacts. Acta Geographica Sinica, 2015, 70(9): 1390-1401. ]

... 0区间的较大门限值作为阈值^[20] ...

2004

0.0

... 对于点过程数据密度的估计,例如时间依赖性的极端事件发生率 λ(t)的计算如下^[21,22]： ...

... Gaussian核函数是应用最广泛的核函数,能够有效利用傅里叶空间并对极端事件发生率 λ(t)产生一个平滑的估计^[21,22]： ...

... ^[21]： pT为POT抽样数据的时间区间 [t1,tm]边界之外的#cod#x0201c ...

... 用Bootstrap技术确定极端事件发生率 λ(t)的置信区间^[21] ...

2003

0.0

... 对于点过程数据密度的估计,例如时间依赖性的极端事件发生率 λ(t)的计算如下^[21,22]： ...

... Gaussian核函数是应用最广泛的核函数,能够有效利用傅里叶空间并对极端事件发生率 λ(t)产生一个平滑的估计^[21,22]： ...

... 采用交叉验证的方法确定窗宽 h^[22] ...

2005

0.0

... GAMLSS（Generalized Additive Models for Location, Scale and Shape）模型被广泛用来构建响应变量和协变量之间的回归关系,并识别最显著的协变量因子^[23,24,25] ...

... 三次立方样条函数被用来作为平滑函数 [ hn(xn,i)],AIC（Akaike Information Criterion）准则用来判别最优模型和最显著协变量,Filliben系数用来判断AIC识别的最优模型的拟合质量^[23,24,25] ...

2012

0.0

姜聪, 熊立华. 基于 GAMLSS 模型的宜昌站年径流序列趋势分析[J]. 地理学报, 2012, 67(11): 1505-1514.

[JIANG

, XIONG L

. Trend analysis for the annual discharge series of the Yangtze River at the Yichang Hydrological Station based on GAMLSS. Acta Geographica Sinica, 2012, 67(11): 1505-1514. ]

... GAMLSS（Generalized Additive Models for Location, Scale and Shape）模型被广泛用来构建响应变量和协变量之间的回归关系,并识别最显著的协变量因子^[23,24,25] ...

2015

0.0

顾西辉, 张强, 王宗志. 1951—2010年珠江流域洪水极值序列平稳性特征研究[J]. 自然资源学报, 2015, 30(5): 824-835.

[GU X

, ZHANG

, WANG Z

. Evaluation on stationarity assumption of annual maximum peak flows during 1951-2010 in the Pearl River Basin. Journal of Natural Resources, 2015, 30(5): 824-835. ]

... GAMLSS（Generalized Additive Models for Location, Scale and Shape）模型被广泛用来构建响应变量和协变量之间的回归关系,并识别最显著的协变量因子^[23,24,25] ...